Grantee Research Project Results
Final Report: "Collaborative Proposal" on Optimal-Control Strategies Based on Comprehensive Modeling and System-Interaction Analyses for Energy-Efficient and Reduced-Emission Fuel-Cell-Energy-Systems: Power Electronics Subsystems
EPA Grant Number: R831581Title: "Collaborative Proposal" on Optimal-Control Strategies Based on Comprehensive Modeling and System-Interaction Analyses for Energy-Efficient and Reduced-Emission Fuel-Cell-Energy-Systems: Power Electronics Subsystems
Investigators: Mazumder, Sudip K. , Nelson, Douglas , Leo, Donald J. , von Spakovsky, Michael R. , McIntyre, Chuck , Herbison, Dan
Institution: University of Illinois at Chicago , Synopsys Inc. , Virginia Tech , University of California - Davis
Current Institution: University of Illinois at Chicago , Synopsys Inc. , University of California - Davis , Virginia Tech
EPA Project Officer: Aja, Hayley
Project Period: February 1, 2004 through January 31, 2007 (Extended to December 31, 2007)
Project Amount: $125,000
RFA: Technology for a Sustainable Environment (2003) RFA Text | Recipients Lists
Research Category: Nanotechnology , Pollution Prevention/Sustainable Development , Sustainable and Healthy Communities
Objective:
In this report, we outline a mechanism for developing an optimal control for power electronic system to enhance the power-management efficiency (Chapter 3). However, it was realized that unlike conventional applications of power converters, which are typically fed by a stiff energy source, a fuel cell is a current-dependent voltage source and hence conventional control approaches may not work. As such, a systematic modeling (Chapter 1) and interaction analysis (Chapter 2) was carried out first to investigate this electrical coupling effect. What emerged is that transient change in load can affect the life of the fuel cell and so can potentially the current ripple. A buffer is required to mitigate the first problem and may require an additional power conditioner. The patent-filed optimal topological control alleviates the need for two separate power conditioner and hence saves footprint space, weight, and cost. It also increases the efficiency flatness via dynamic power management of the multi-modular architecture. The increase in efficiency has implications for the enhanced life of the fuel-cell stack as well as other emissions. Although not shown explicitly, the topological architecture can be modified for low-frequency-ripple mitigation that also directly addresses stack life, sizing, and efficiency. Overall, the theoretical work has been validated with detailed experimentations and two patents have been filed. Besides, 2 peer-reviewed international journal and 2 IEEE Conference papers have been published.Summary/Accomplishments (Outputs/Outcomes):
1. COMPREHENSIVE MODELING OF FUEL CELL POWER CONDITIONING SYSTEM
A. Outline
A comprehensive model of the planar PCS needs to meet the following objectives, i) resolve PSOFC power-system interactions and dynamics, and develop design insights towards the achievement of reliable system configurations, ii) enable study of interaction analysis, control, and optimization on a low cost modeling platform without the need of a supercomputer. Moreover, with faster simulation capability, this may lead to the real time simulation thereby enabling the study of long-term reliability.
Comprehensive mathematical models for each of the subsystems are developed, and integrated in a common platform to obtain the system model. The issues with the integration of the system model is identified and discussed. A reduced order system model is developed to address the issues of simulation.
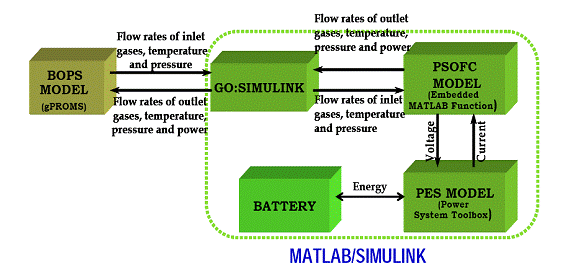
Figure 2.1: Schematic shows the modeling framework for a comprehensive PSOFC based PCS modeling framework.
Figure 2.1, shows the proposed comprehensive modeling framework. The system models comprise PSOFC, BOPS, PES, and the battery bank. The flow of various parameters among the subsystems, as shown in the Figure 2.1, is ensured to ascertain proper system interaction. The comprehensive model requires two low-cost softwares for implementation (Simulink/Matlab including SimPowerSystem and gPROMS1 including gO:SIMULINK2).
B. PES Modeling
Residential PES Model
The PES topological model for a 5 kW residential application is shown in Figure 2.2. The model essentially consists of a dc-dc boost converter to step-up the PSOFC output voltage to an intermediate dc bus voltage (220 V). A dc-ac inverter is used to convert the dc bus voltage to feed power to the ac load.
The rated voltage of the PSOFC stack is between 70 – 90 V. As such, the front-end dc-dc converter for the 5 kW has to be unidirectional (because current should not flow into the fuel cell) and should step-up the voltage, which regulates the output voltage at 220 V. A single-switch unidirectional boost converter, as shown in Figure 2.2, would meet the requirements. The operational details of the boost converter are outlined in (Mohan et al., 1995). When the switch Sw is turned on, energy is built in the inductor L1, and when the switch is turned off the stored energy in the inductor is transferred to the output. The duty ratio of the switch is controlled to attain the desired output voltage.
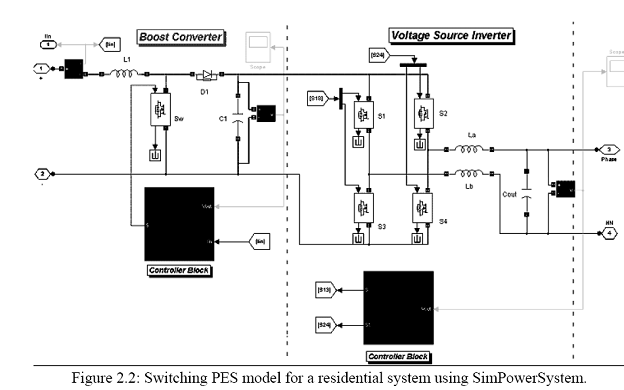
For the dc-ac inverter a full-bridge voltage source inverter is chosen for its simpler design and operation. The operational details of the converter and the control are outlined in (Mohan et al., 1995). A sinusoidally-modulated switching sequence is generated for S1 (S3) and S2 (S4) to obtain an averaged sine wave at the output of the VSI. S1 (S2) and S3 (S4) operate in a complementary order.
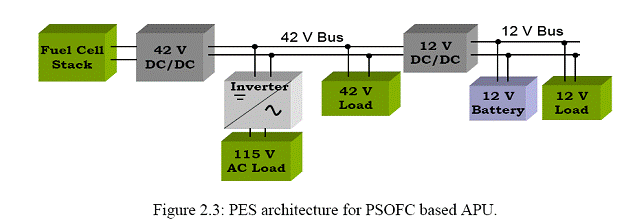
PES Modeling for Vehicular Auxiliary Power Unit (APU)
The architecture of the PES topological model for the APU is shown in Figure 2.3. The model essentially consists of a dc-dc buck-derived converter to step-down the PSOFC output voltage to an intermediate dc bus voltage (42 V). An inverter is used to convert the dc bus voltage to feed the ac power bus. Further, the intermediate dc bus voltage is stepped down using a bidirectional converter to supply the 12 V dc loads and to charge the battery.
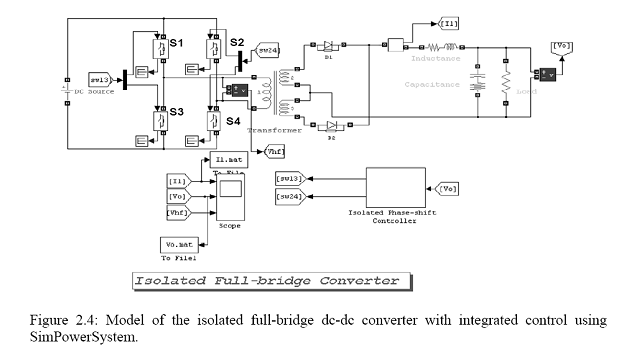
The rated voltage of the PSOFC stack is between 72–90 V. As such, the front-end 42V dc-dc converter for the 5 kW APU has to be unidirectional (because current should not flow into the fuel cell) and a step-down converter, which regulates the output voltage at 42 V. A full-bridge converter, as shown in Figure 2.4, is chosen to meet the requirements. The operational details and control design of the converter are outlined in (Redl et al., 1990). The switches S1 and S3 and S2 and S4 switch in complementary pairs, with a time delay between the switching of S1 (S3) and S2 (S4). This phase delay between the switching signals of S1 (S3) and S2 (S4) is controlled to obtain the desired output voltage.
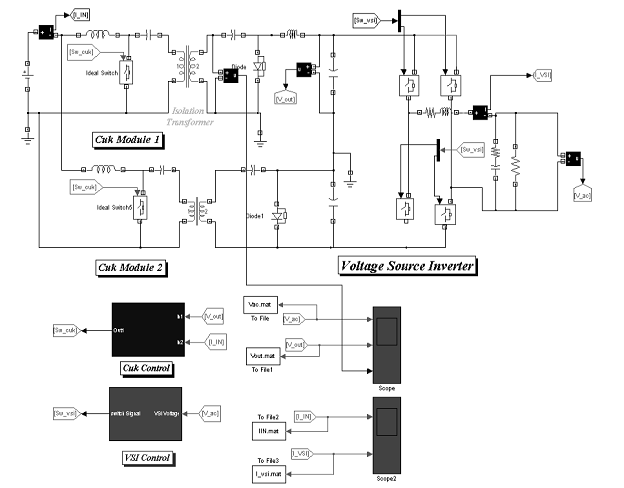
Figure 2.5: Switching model of the dc-ac inverter which consists of two-module parallel Ćuk converters followed by a full-bridge VSI.
PSOFC Spatio-temporal Modeling
For accurate prediction of the effects of system interactions on the PSOFC, one needs to analyze the PSOFC internal parametric variations (Ferguson, 1991; Erdle et al., 1991; Hartvigsen et al., 1993; Yentekakis et al., 1993; Hendrikson et al., 1994; Ferguson et al., 1996). Because a transient model of the SOFC (e.g., (Mazumder et al., 2004)) cannot predict the spatial dynamics, a spatio-temporal electro-thermo-chemical model of the PSOFC (in Simulink) is developed, which provides spatial discretizations of the cell. This model is designed to accept required system inputs (reactant stream flow rates, compositions, and temperatures, cell geometric parameters, and cell current) and computes the corresponding spatial properties of a cell.
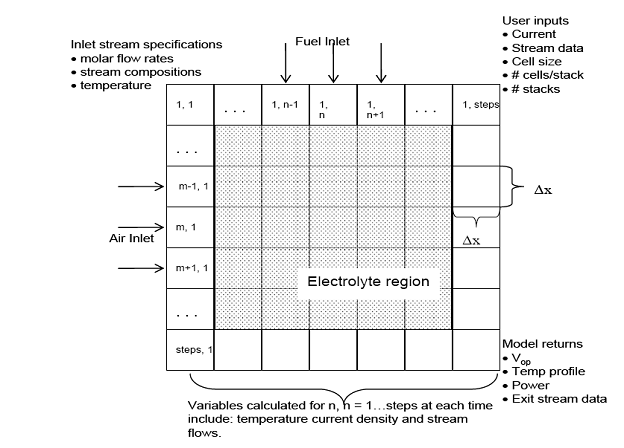
Figure 2.6: Spatial homogenous model for the PSOFC providing two-dimensional discretizations involving finite-difference method.
The cell temperature (T) in the two-dimensional (x and y) model, as shown in Figure 2.6, is computed from the time-dependent solution of the following equation:
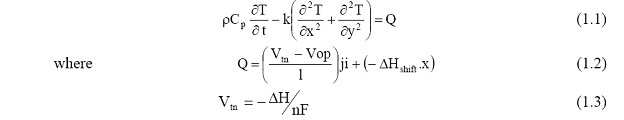
where Vtn is the thermal neutral voltage, Vop is the operating voltage, ji is the current density, ρ is the mass density of the control volume, Cp is the combined specific heat at constant pressure, l is the cell thickness, ΔHshift is the enthalpy of the shift reaction in the control volume, ΔH is the enthalpy of the main reaction, n is the molar flow rate of the fuel and k is the thermal conductivity of the fuel cell. To approximate the second-order partial-differential equation, a finite-difference method using central differences (Constantinides, 1999) is used.
By approximating ∂T/∂t as a simple forward difference and substituting [(Tj+1-Tj)/Δt] for ∂T/∂t, substituting (1.2) into (1.1), and marching the solution through time yields the Euler’s explicitintegration scheme for the determination the spatial temperature variation. With the step
size Δx = Δy , the expression for temperature becomes
In the course of each of the iteration, the assumed operating voltage is used to determine the current density in each of the control volumes throughout the cell using

where ASRm,n is the local temperature-dependent area-specific resistance and Enm,n is the Nernst potential defined as

ΔG is the change in the Gibb’s free energy. The current density as in (1.6) is then summed to compute the total cell current:
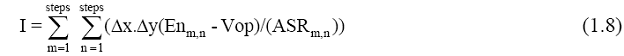
These local current-flux values are used to determine the change in stream composition based on the reaction in each control volume:
The fuel exit-composition of each control volume is equilibrated with respect to the shift reaction before entering the downstream control volume:
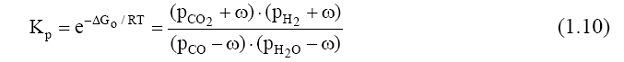
where ΔGo is a temperature-dependent variable, pCO2, pH2, pCO , and H2O p are the partial pressures of CO2, H2, CO, and H2O, respectively, Kp is the constant of equilibrium, R is the universal gas constant, and ω is the adjust in the gas compositions due to the shift reaction. Equation (1.10) is used to adjust the compositions to enforce the shift equilibrium constraint at the entrance to each control volume
BOPS Modeling
The configuration of the BOPS model for the PSOFC stack is shown in Figure 2.7. The analytical model is implemented in gPROMS. The comprehensive details of the initial configuration are provided in (Mazumder et al., 2004; Rancruel, 2005).
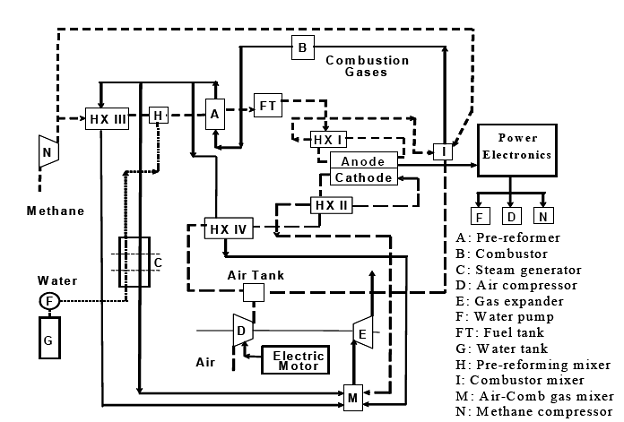
Figure 2.7: Schematic of the comprehensive BOPS model.
Briefly, the BOPS model comprises a set of first principle and semi-empirical equations for component and subsystem mass and energy conservation, system kinetics, and geometry for both design and off-design operation. A sampling of some of these equations for a number of principal BOPS components are outlined as follows.
Modeling of the Steam Methane Reformer
A set of simplifying assumptions are introduced to facilitate the modeling of the steam-methane reformer. A single reactor tube is analyzed as in Figure 2.8. Thus, all the tubes in the reactor behave independent of each other. Reforming and combustion gases are assumed to behave ideally in all sections of the reactor. The demethanation and water gas-shift reactions are kinetically controlled but are constrained by equilibrium considerations. It is assumed that no carbon deposition is allowed in the SMR reactor. The axial dispersion and radial gradients (plug flow conditions) are neglected.
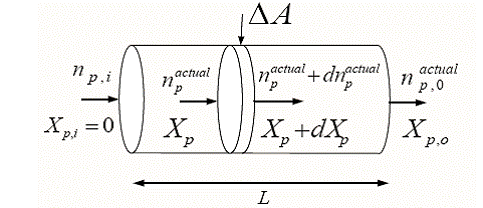
Figure 2.8: Reactor tube model of the steam methane reformer.
The dynamic mass balance on the reformate gas side is given by

where C is the methane molar concentration (g-mole/m3), U the superficial velocity, Ra is the methane reaction rate per unit mass of catalyst, c ρ is the catalyst bed density and x is the axial direction.
The reformat gas side energy balance is as follows:
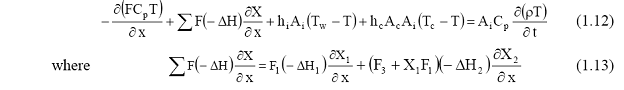
In this balance equation, Cp is the specific heat at constant pressure of the tube-side, Ac is the external surface area of particles per volume of catalyst bed, Tc is the catalyst temperature, hi is the inside heat transfer coefficient, hc is the catalyst-fluid heat transfer coefficient, ΔH1 the demethanation reaction enthalpy, and ΔH2 is the water-gas shift reaction enthalpy. In Equations 2.12 and 2.13, X1 and X2 represent the conversions of the demethanation and water-gas shift reactions, respectively. After spatial discretization, the reaction enthalpies are evaluated at each reactor segment’s average temperature.
Modeling of the Compact Heat Exchangers
The heat exchangers used in the BOPS configuration are all plate-fin type, compact heat exchangers with a single-pass, cross-flow arrangement. Their modeling details are presented in (Rancruel, 2005). The heat transfer and pressure drop models used are based on the work of Shah, (1981) and Kays and London, (1998). The effectiveness-NTU method is applied in order to relate the geometric models of the heat exchangers to the thermodynamic ones. The expression for the heat exchanger effectiveness is obtained as in (Mazumder et al., 2004) and is valid for single-pass, cross-flow arrangements with both fluids unmixed.
The energy analysis of each discretized section of the heat exchanger is given by
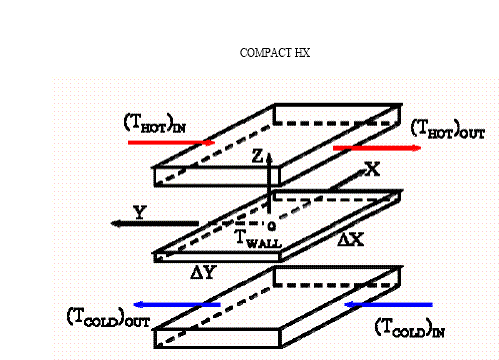
Figure 2.9: Spatial discrete model of the heat exchanger.
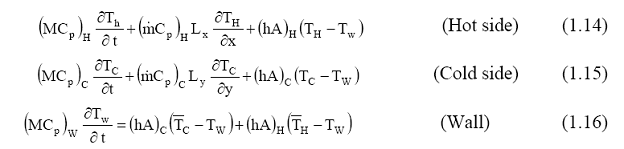
where M is the mass in the control volume, subscripts C and H indicate the cold and hot sides, subscript W the wall, and x and y are the longitudinal and transverse directions, respectively. A refers to the heat transfer area while h refers to the heat transfer coefficients.
Modeling of the Methane and Air Compressors
In the compressor, heat flows from the fluid to the casing to the ambient as well as from the fluid to the impeller to the casing to the ambient through the bearings, seals, and shaft. The thermal capacitance of the casing, impeller, and inlet duct can be approximated by a single thermal mode at a temperature To such that
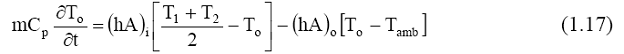
where m is the mass of the thermal mode, Cp is the thermal mode specific heat, ( )hA i is the inner conductance from the fluid to the thermal mode, ( )hA o is the outer conductance from the thermal mode to the ambient, and To is the thermal mode temperature.
The shaft component is used to compute the turbo machinery rotational speed (N) based on input values of turbine power output and compressor power input. A power balance yields

where I is the moment of inertia and ΔW is the power balance on the component. The transient heat transfer model for an expander is similar to that for compressors and scalable performance maps are used for both types of components to simulate off-design behavior.
C. System Integration
All the component models are built on their best possible modeling platform, and are optimized to yield best results during the individual subsystem simulation. However, several issues have been encountered during the integration of the individual subsystems. These can be classified into A) modeling issues and B) simulation issues.
Modeling Issues
1. Bulky BOPS model in gPROMS needs an gO:Simulink interface for data transfer between matlab/simulink and gPROMS. To ensure proper data exchange between the gPROMS and the matlab/simulink, input and output ports need to be created in the gPROMS based BOPS model and the input and output variables needed to be assigned to the respective ports.
2. To interface with the PES model, the PSOFC stack model needs to be a voltage source. However, conventional PSOFC stacks are modeled as voltage-controlled current source. Therefore, the PSOFC stack has to be remodeled to behave as a current-controlled voltage source. Now, the amount of current drawn should to be provided as information to the stack from the PES to calculate the stack voltage.
Issues with Simulation
1. The Bulky BOPS Model (very high order) significantly increases the computational overhead for the system simulation. Since the PES and the PSOFC stack models have significantly faster response and needed to be sampled at very high sampling rate (order of tens of microseconds). In the comprehensive model, the bulky BOPS model also gets sampled at this rate, which makes the system simulation extremely slow. To prevent this condition and hence to accelerate the simulation, each individual subsystem needs to sampled individually at its own rate depending on the response time.
2. With significant difference in the response time of the individual subsystem models, ensuring the integrity of data exchange among the subsystems running at their individual pace in their own platforms becomes an issue. Rate transition blocks are used to ensure date integrity in presence of multiple sampling rates.
3. The PES model consists of several switching converters. The switches with discontinuous states, lead to discontinuous-differential equations. Again the presence of the control feedbacks leads to algebraic loops in the model which need to be solved iteratively. A stiff solver and fast sampling is required for convergence and numerical stability. Numerical solver “ode23tb” is used to solve the crude error tolerances at the point of discontinuity and to solve the stiff differential equations with algebraic loops.
D. Reduced Order Modeling
The BOPS subsystem model consists of hundreds of components and subcomponents, and the order of the subsystem is very high. This order of the BOPS model (450 approx.) significantly increases the computational overhead for the system simulation. An added reason for higher computation time is the need for interfacing between the gPROMS and Simulink/Matlab models via the gO:Simulink interface. Again, in the integrated system, each of the subsystem needs to run at the maximum possible sampling time step, which is decided by the subsystem (the PES) that needs to run at the smallest time step. With such a small time step, the BOPS is found to be the bottleneck for the progress of the simulation.
As such, the prime need is to reduce the order of the BOPS model and implement the approximate model in the Simulink/Matlab platform to reduce computational time. Figure 2.10 shows the reduced-order modeling framework for the PSOFC PCS. The reduced order BOPS model is implemented in simulink using polynomial approximation making it all MATLAB/ Simulink system model. This enables the usage of Real Time Workshop (Mathworks) for realtime simulation.
PES Average Modeling
Because the PES switching model comprises discontinuous-differential equations, a stiff solver and fast sampling is required for convergence and numerical stability. For example, to solve the switching model of a PES converter operating at 20 kHz (i.e., a switching period of 50 μsec), sampling time as low as hundreds of nanoseconds may be required. Comparing that to the vastly different (typical) sampling times of PSOFC and BOPS models (which are around few milliseconds and hundreds of milliseconds, respectively), it is realized that the PES switching model is one of the key hindrances to the fast computation of PSOFC PCS model.
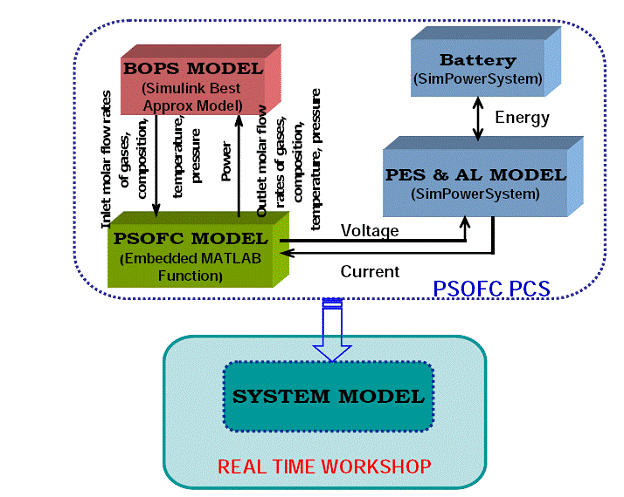
Figure 2.10: Reduced-order modeling framework for PSOFC based PCS, developed in Simulink /MATLAB platform, thereby enabling real-time simulation of the system.
Obviously, to increase the speed of the PCS simulation, the need is to avoid discontinuity, thereby reducing the sampling rate and bring it as close as possible to that required by the PSOFC and BOPS models without significantly compromising the accuracy. In one such approach (Khaleel et al., 2004), the PES is designed as a power converter with a constantefficiency module, where output of the converter is a fixed fraction of the input power. However, this model is inaccurate as it assumes that the efficiency of the PES is constant for all load conditions. Further, and more importantly, this model does not predict the transient response of the PES.
An alternate approach to avoid discontinuity of the PES model is to use a map (Mazumder et al., 2001). In a map, instead of solving the switching differential as a whole, the overall model is solved in finite time intervals by treating the PES as a piecewise-linear system (PLS). Subsequently, using the commutative property, the solution is pieced together in each of intervals to construct the final solution in terms of the initial conditions of the states of the PES model. Although a map is a powerful and accurate approach, it typically requires the knowledge of the analytical solution of the PLS and the complexity of the solution increases with the order of the PES model.
An averaged-modeling technique (Lee, 1990; Middlebrook and Ćuk, 1977) is adopted which enables us to analyze the behavior of the PES without significant computational overhead. Figures 2.11 and 2.12 shows the averaged models of the PES converters in equivalent-circuit form (Lee, 1990). One can notice that unlike the switching models, the averaged models do not have any discontinuous elements. Further, the averaged (circuit) models enable the usage of built-in circuit modules in Simulink.

Figure 2.11: Switching average model (AM) of the boost converter.
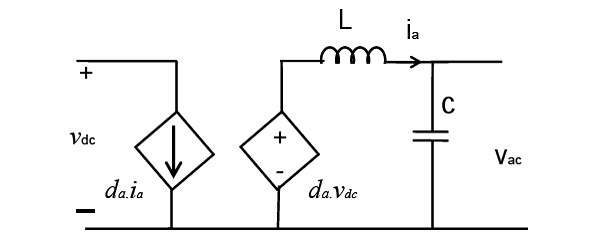
Figure 2.12: Average model of single-phase full-bridge VSI (L = La + Lb).
Boost converter
For a boost converter, the switching average model is obtained by averaging the state equations for the whole switching period.
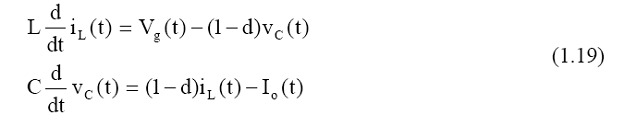
where iL(t), vC(t) are the inductor current and capacitor voltage respectively. Vg(t) is the input
voltage of the converter and Io(t) is the output current of the converter.
Voltage Source Inverter
For a VSI, the switching average model is obtained by averaging the state equations for the complete switching period.
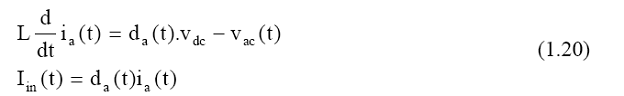
where ia(t) is the inductor current, vdc is the dc input voltage, Iin(t) is the input current, vac(t) is the output ac voltage of the VSI, and da(t) is the PWM duty-ratio of the inverter given as
From Figure 2.13, it can be noted that, an averaged model ideally provides the averaged dynamics of the PES and as such, it transforms the PES model from a discontinuous to a smooth form. The accuracy of the averaged model typically varies with the switching frequency, with higher accuracy for higher operating frequency.
Table I shows that the responses of the average models are significantly accurate, while the reduction in the simulation time is of the order of hundreds. The average models do not have any switching dynamics, and hence, it cannot predict the effect of high frequency switching ripple on the PSOFC stack. However, the average models, that accurately represent their switching models with such a level of increase in their simulation speed, enabled the long-term simulation of the complete PSOFC PCS.
TABLE I: Accuracy and Reduction in the Computational of the Average Models as Compared to the Switching Models

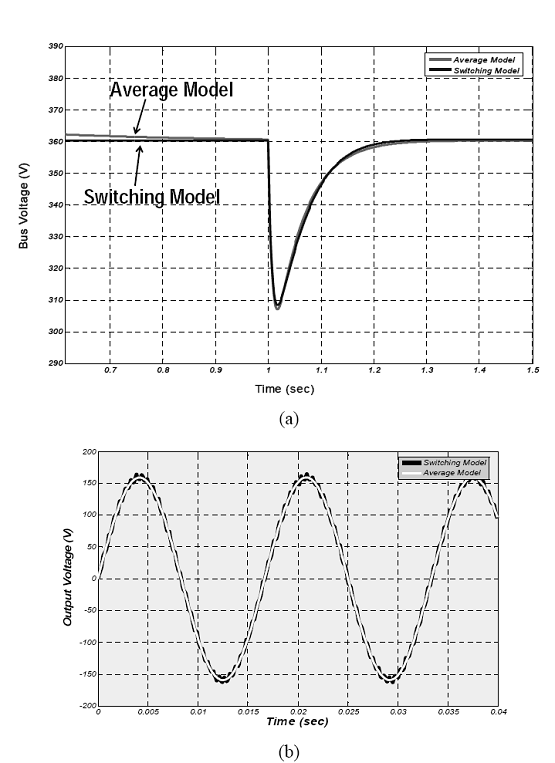
Figure 2.13: Accuracy of the PES average models, illustrated by comparing the averaged dynamics with their switching dynamics for (a) the dc-dc boost converter (when subjected to a load transient at t = 1 sec), and (b) voltage source inverter.
One-Dimensional PSOFC Model
The PSOFC subsystem, is usually designed as a voltage controlled current source, that is, it derives the current to be delivered to the load based on the output voltage of the cell. However, the PES, which consists of several power converters, are designed to be powered by voltage sources. Hence, the spatial domain cell subsystem is modified to affect the same. However, in doing so, the model has to solve for the voltage iteratively, which is again an overhead for the simulator. With spatial domain computation for each of the properties inside it for each finite time step (order of milliseconds), the simulation speed is reported to be significantly low.
Hence to hasten the simulation one-dimensional PSOFC model is derived from the two dimensional model. Figure 2.14 shows the homogenous discrete slab representation of the model by reduction in the (y) dimension. Using the homogeneous slab model for the PSOFC, the onedimensional spatio-temporal model of the PSOFC is derived from its two-dimensional form (i.e., equations (1.1)-(1.10)) by discretizing only in one dimension (x). The corresponding equations of the one-dimensional PSOFC model are tabulated in Table II. Figure 2.15 shows the comparison of the two dimensional (2D) model and the one dimensional (1D) model subjected to load transient. The accuracy of the one-dimensional model is quite appreciable (error of 5.2%) as compared to the two dimensional model. The significant reduction (approximately 57.15%) of the computational time for the 1D model speaks for its advantage for the interaction analysis study.
Figure 2.14: One-dimensional homogenous slab model for PSOFC providing discretizations involving finite-difference method.
TABLE II: Summary of the One-Dimensional Model (Derived from Spatial Model)

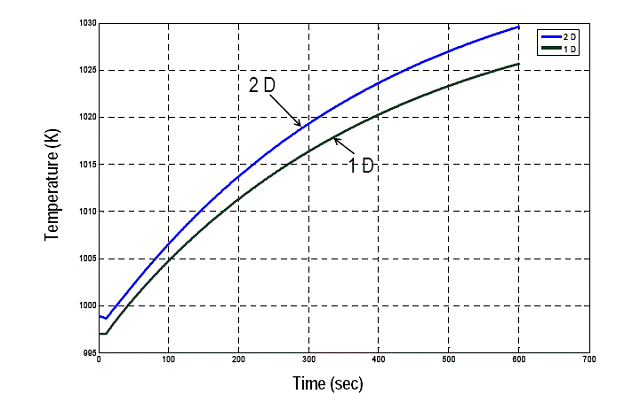
Figure 2.15: Comparison of the mean cell temperature of the PSOFC (when subjected to the load transient at t = 10 sec) obtained using its one- and two-dimensional models.
Polynomial-Approximation BOPS Model
To realize the polynomial-approximation model, first, the BOPS model is subjected to different sets of load transient and steady-state electrical feedbacks and stored the transient responses of all the output BOPS parameters (such as temperature, air and fuel flow rates, and air and fuel compositions). These parameters are used to interface the BOPS model to the PSOFC model. Subsequently, multi-order (starting from linear to seventh-order) polynomial approximations on each set of these data are applied to obtain the closest approximation that provides optimal compromise between speed of simulation and accuracy with regard to the data obtained using the comprehensive model. In (Khaleel et al., 2004), a similar approach is adopted to reduce the order of the BOPS model.
In Figure 2.16, a polynomial approximation of the BOPS response is illustrated. The order of polynomial is chosen, which maximizes the accuracy of the approximation model and minimizes time for simulation. The result of accuracy and the simulation with that of the time for different order of approximation as compared to the comprehensive model is given in Table III. A fifthorder polynomial approximation was chosen to achieve the optimal compromise between simulation speed and accuracy.
TABLE III: Computational Overhead And Accuracy Comparison Of The Polynomial Approximation

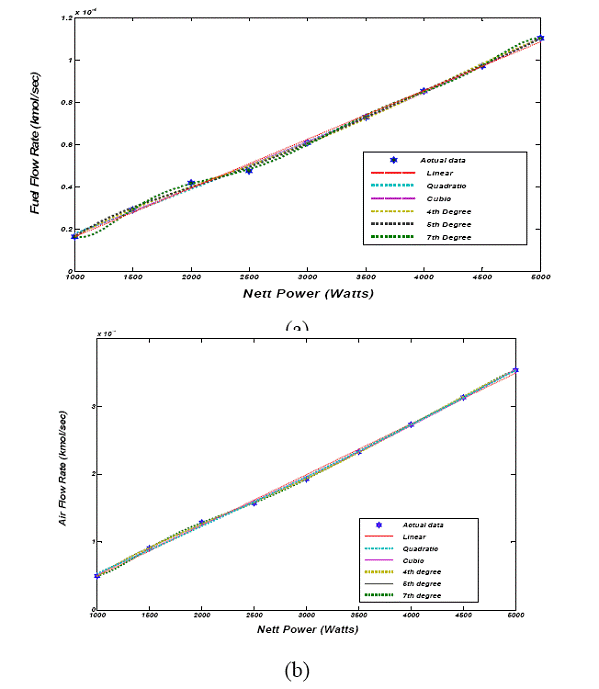
Figure 2.16: Polynomial approximation of the air- and fuel-flow rates of the BOPS model vs. net power.
E. Experimental Model Validation
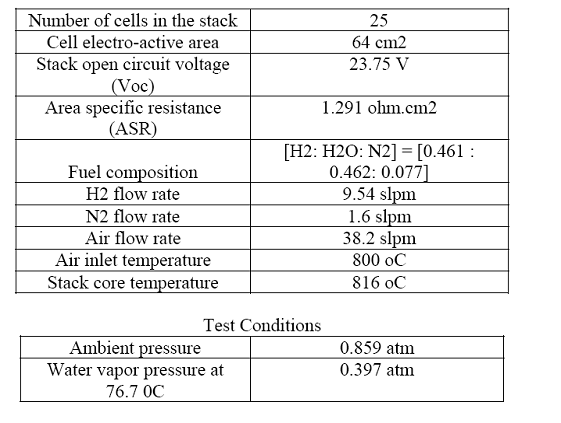
The effect of electrical feedbacks on PSOFCs is studied on the stack prototype, as shown in Figure 2.17(a), consisting of 25 planar cells in series. The PSOFC stack is built at Ceramatec Inc. In the stack, all the planar cells are mounted in a single manifold. The cross-flow arrangement for the reactants in the stack is illustrated in Fig. 2.17(b). Each cell has an electro-active area of 64 cm2. The ASR of the individual PSOFC for the models at any core temperature are obtained using the empirical formula
where T is the stack core temperature, which depends on the flow rates and temperature of the inlet gases and the stack fuel utilization, the constants A and B are obtained experimentally from the stack characteristics.
Similarly, the 1-D and 2-D model calculates the specific heat capacity and cell density based on the core temperature and experimentally determined constants. The detail specification and the test condition of the stack are given in Table IV and V.
TABLE IV: PES Specifications
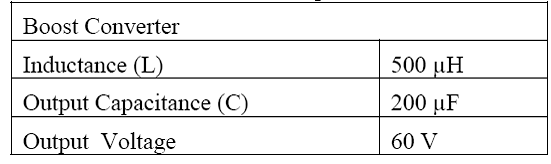
TABLE V: PSOFC Stack Specifications and Test Conditions
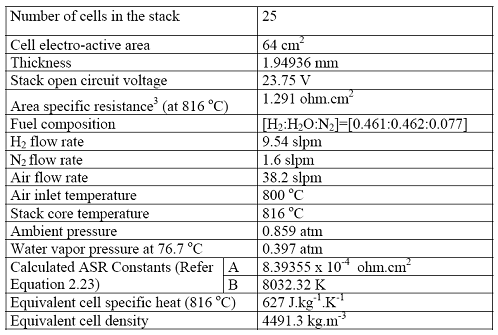

Figure 2.17: a) Experimental setup of the 25 cell PSOFC stack with the PES and b) The PSOFC stack manifold and the arrangements for air and fuel flow.
Figure 2.18: Setup for the stack characterization and load transient test.
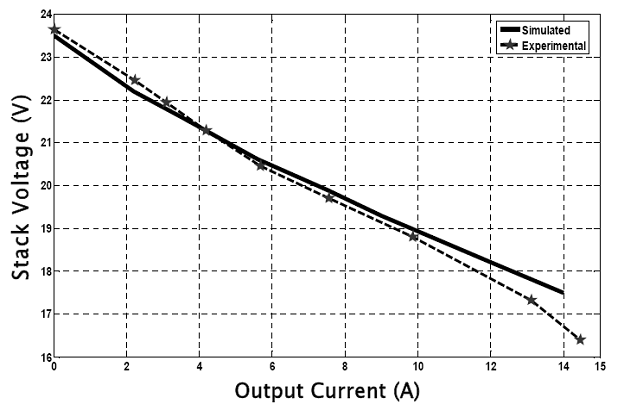
Figure 2.19: Steady-state I~V characteristics comparison of the planar SOFC stack.
Steady-state Characteristics of the PSOFC Stack
Figure 2.18 shows the setup for the characterization of the stack. The dc electronic load is varied in steps to draw different amount of current from the stack. The voltages of the stack at different current levels are noted using the oscilloscope. Comparison of I~V characteristics of the 25 cell stack model and the experimental unit, as shown in Fig. 2.19, shows the accuracy of the analytical model in the steady-state.
Model Validation during the Transients
To prove the accuracy of the model during the transient, the stack is subjected to electrical load transients and low frequency ripple. The connection arrangements and the response comparisons are discussed as follows. Response to the Load Transient
The effects of load transient on the output of the PSOFC stack are analyzed. The dc electronic load operating in constant current mode is connected across the stack output, as shown in Figure 2.18. The dc electronic load is programmed to apply a current transient from 2.2 A to 12 A and subsequently 12 A to 2.2 A, after 1400 seconds. Figs. 2.20(a) and 2.20(b) shows the drop in the output voltage of the 1-D stack model and the experimental stack prototype respectively. Hence, the 1-D stack model accurately emulates the electrical characteristics of the stack.
Due to the subjected load transient, the mean temperature in the stack increases as shown in Fig. 2.21. (The mean temperature profile near the no-load to full-load transient is skewed due to manual turning off of the electronic load at t = 2000 sec accidentally, and is emulated in the stack model during the simulation). From Figure 2.21, it can be noted that the 2D model more closely follows the experimental stack temperature as compared to the 1D Model.
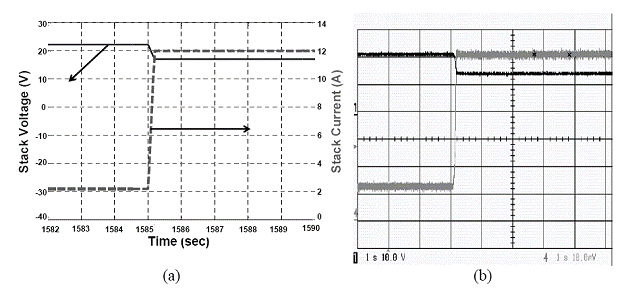
Figure 2.20: Effect of load current transient (2.2 A to 12 A) on the voltage of a) the stack model and b) experimental planar stack, scope channel 1 (10 V /div) and channel 4 (2 A/div) measures the stack voltage and current respectively.
Response to the Low-Frequency Ripple
Figure 2.22 shows the setup to study the effect of the ripple on the stack. The PES consists of a bidirectional dc-dc boost converter. The switch of the converter is modulated using a biased sine wave reference at 60 Hz, generated using the signal generator. To observe various percentage of the ripple in the current, the bias and the amplitude of the sine wave is varied. The current drawn from the stack contains 120 Hz ripple. The load connected across the boost converter is adjusted so that the magnitude of the ripple is 40 percent of the mean stack current. Figures 2.23(a) and 2.23(b) shows the effect of a low frequency (120 Hz) ripple on the 1D stack model and the experimental prototype respectively, which validates the electrical response of the stack model.
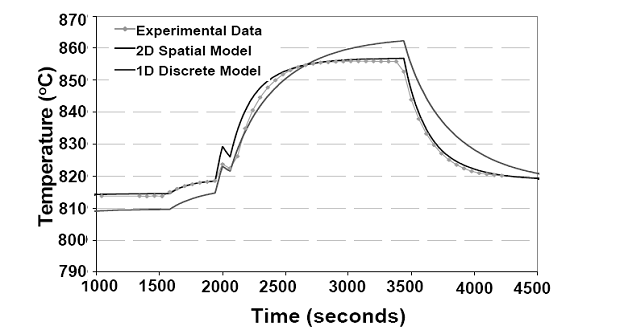
Figure 2.21: Validation of the effect of load transient (no load (NL) – full load (FL) – no load (NL)) on the planar SOFC stack temperature. Actual no load to full load transient occurs at 2077 seconds.
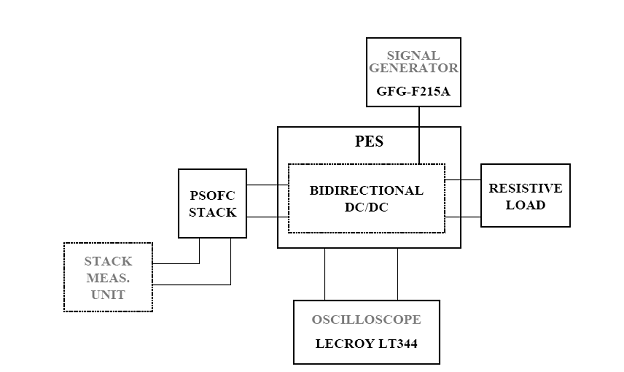
Figure 2.22: Setup to study the effect of the ripple on the stack.
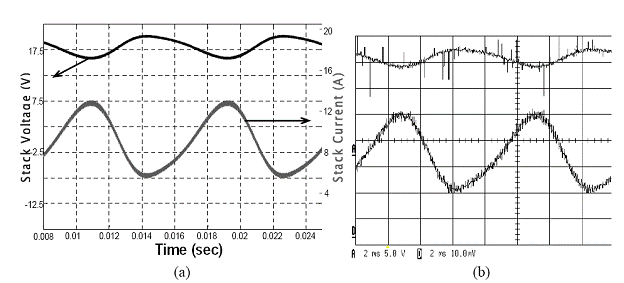
Fig. 2.23: a) Effect of 40 percent current ripple on the stack voltage of the model. b) Experimental validation of the ripple effect on planar SOFC stack, scope channels A and D show the stack voltage and current respectively.
2. SYSTEM INTERACTION ANALYSES
A. Outline
Planar solid-oxide fuel cells (PSOFCs) are promising candidates for future alternative-energy-based power systems because of their high energy-conversion efficiency, high fuel flexibility, and tolerance to the fuel impurities [1-3]. However, the high cost of production and issues with the reliability have been bottlenecks in the commercialization of the PSOFC and PSOFC based power-conditioning system (PCS) as well.
Several studies have addressed the issues related to the reliability of SOFC. Effects of higher operating temperature and high fuel utilization on the material properties of SOFC have been reported earlier [4, 5]. These studies on SOFC have primarily focused on studying the effects of material properties and electro-kinetics of chemical reactions on cell operating life and performance. However, there is a need to study the impact of the electrically-induced feedback effects (induced due to the PES and the ALs) on the PSOFC performance.
Achenbach [6] and Hartvigsen et al. [7] have demonstrated preliminary results on the impacts of linear electrical load impedance and their change on the dynamics of a SOFC. Acharya et al. [9, 10] and Mazumder et al. [11] have demonstrated effects on the performance and durability of a tubular SOFC (TSOFC) stack. Recently, Gemmen [8] attempted to estimate the effects of electrical loads and inverter current ripple on the performance of proton-exchange membrane (PEM) fuel cells using a simple first-order model of a PES. As investigated in [8, 9, 11], the dcac inverter ripple currents may have a degrading impact on the fuel-cell performance if not adequately controlled.
However, no study had been reported to estimate the effects of such electrical feedbacks on the planar SOFC. Again, the impact of several other electrical feedbacks such as the load power factor, harmonic distortion, and the nature of load transients on the performance and reliability of any fuel cell system are not investigated. Therefore, in this paper, using a transient system model comprising a two-dimensional and spatio-temporal PSOFC model and a nonlinear PES model, we investigate the impacts of PES and AL induced electrical effects on the performance of the PSOFC. The steady-state and transient predictions of the cell model are experimentally validated. Subsequently, using this validated model, parametric analyses on the impacts of transience, power factor, and distortion of the application load as well as low-frequency current ripple is conducted. Finally, we demonstrate (experimentally) the long-term impact of two most significant electrical feedbacks on the area-specific resistance and the corresponding loss of effective stack power. We consider two types of electrical feedbacks: those that are induced by the power electronics and those that are induced by the application load.
B. Power-electronics-induced Feedbacks
Low-frequency Ripple
A single-phase fuel-cell dc-ac converter (also known as inverter as shown in Fig. 1) for

Journal Articles on this Report : 2 Displayed | Download in RIS Format
2004
2005
2006
Conclusions:
In this chapter, a comprehensive spatio-temporal model of the PSOFC PCS is developed which enables the study of interactions among various subsystems. However, the bulky BOPS model with hundreds of components and subcomponents turn out to be a major bottleneck for the system simulation. The PES model, being a high frequency switching discontinuous system, slows down the speed of simulation of the integrated system model. Hence to increase the speed of simulation reduction of the subsystem models to obtain simpler models with lower order and devoid of switching discontinuity are essential. The reduced PES model obtained by averaging the switching states leading to a continuous subsystem is found to follow the response of the switching model with appreciable accuracy, while increasing the speed of the simulation significantly. The stack model is reduced by reducing the spatial model in one of the dimension to obtain 1D discrete model. A multi-order polynomial approximation of the BOPS model closely follows the steady state response of the analytical model. The resulting reduced-order model has improved the simulation speed of the system with very high accuracy.
The model validation experiments show that the response of the analytical models closely follow the experimental result. While the faster 1D model electrical characteristics emulate the response of the experimental prototype in the steady state and in the transient, the 2D model is highly accurate in predicting the thermal response of the PSOFC stack. Therefore, these models when used selectively, can accurately predict the dynamics of an actual PSOFC stack, enabling the interaction analysis and thereby the control design and optimization an achievable goal in a finite time.
We delineate several different electrical feedbacks induced due to the power electronics subsystem (PES) and the application load (AL), which may potentially affect the performance and durability of planar solid-oxide fuel cell stack (PSOFCS). To analyze the impact of such feedbacks, a comprehensive, spatio-temporal, and numerical system model is developed. The accuracy of the model and their ability in determining the effects of several electrical feedbacks on PSOFC during the transient and in the steady state are experimentally validated. Using the validated model accurate estimations of the impacts of several electrical feedback effects on the performance and durability of the PSOFC PCS is conducted using parametric study. An experimental degradation study is done to estimate the long-term effects of the load transient and the ripple on the performance of the stack. Specifically, we conclude the following:
· The no-load to full-load transient increases the current density in the planar fuel cell abruptly and immediately. The higher level of current density increases the fuel utilization and the polarization voltage leading to a drop in the cell voltage. This change in the fuel utilization is detrimental to the cell performance and efficiency;
· The load transient not only increases the mean temperature but also changes the spatial distribution of stack temperature. This variation depends on the magnitude of the current transient and is independent of the slew rate of the transient;
· The load transients accelerate the degradation of the area specific resistance (ASR) of the planar cell. Therefore, they deteriorate the efficiency of the stack. To prevent this, suitable energy buffering techniques should be available to eliminate the effect of the load transient from the stack;
· The higher ripple current magnitude in the stack current forces to decrease the operating fuel utilization of the stack, and hence, lowers the stack efficiency. However, this has negligible impact on the stack temperature;
· In the long term, the ripple current accelerates the degradation of the ASR, deteriorating the efficiency of the stack;
· Lower power factor of the load increases the magnitude of current ripple drawn from the stack. And this reduces the efficiency of the stack. The effect of the load power factor on the stack temperature is minimal;
· Higher THD of the ac load decreases the magnitude of current ripple drawn from the stack. However, it has negligible impact on the stack temperature.
The parametric study in the paper provides a detailed insight into the effects of several electrical-feedback effects on the planar solid-oxide fuel cell (PSOFC) stack and the PSOFC power conditioning system (PCS) as a whole. This will facilitate the design of control and optimization of PSOFC PCS parameters towards the achievement of a highly-efficient and reliable power system.
A power-management control system based on distributed power-electronics subsystem (PES) for a fuel-cell based energy system is outlined. Unlike the conventional approach, which typically uses a lumped PES unit for interfacing the stack to the application load, the distributed PES has multiple modules, which can be controlled and selectively activated depending on the load demand. Of the N distributed modules, up to N-1 can be connected to the fuel-cell-stack or the battery under steady-state or transient condition, while the Nth converter is connected to the battery for charging even under full-load condition. For part-load operation, additional modules can be used for battery charging as well. Thus, the need for a dedicated full-power-rating battery converter (as in conventional approach) is significantly minimized. As the load demand increases, an optimal criterion determines the number of such modules that need to be activated for maximum PES energy-conversion efficiency that in return leads to enhanced stack utilization. This optimal criterion has been developed using a convex optimization framework. Although this paper outlines an analytical formulation of the optimization function (representing the overall loss of the PES), the coefficients for the optimization function can be determined experimentally as well by simply mapping the loss (with varying power demand) as a function of the input current. Further, since the power-management scheme relies on selection of optimal number of active modules following change in load demand, a reaching criterion has been developed to ensure the post-load-transient stability of the PES. The reaching criterion uses a multiple-Lyapunov-function based methodology and determination of the convergence of PES dynamics simply requires solving a matrix inequality. Predictions of both the optimal criterion and the reaching criterion have been validated. The results show that the optimal power 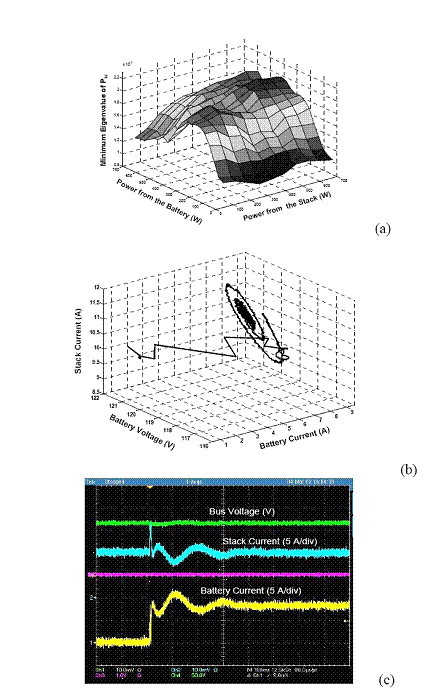

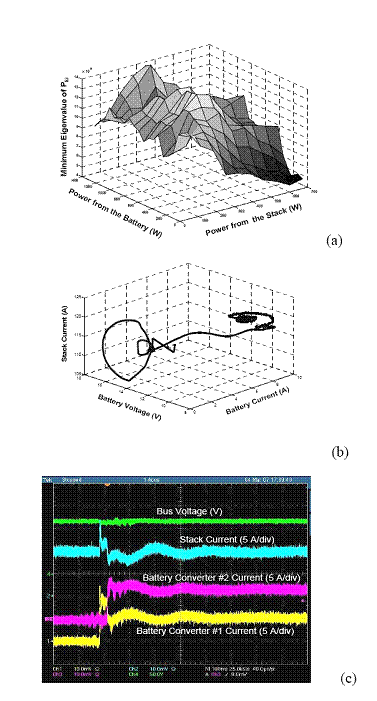
Fig. 4: Post-transient stability of the distributed PES after a load transient from 0.6 kW to 1 kW. Initially one module feeds the load from the stack and subsequently after the transient, a second module is activated that feeds the additional power from the battery. (a) Minimum eigenvalue of Pki > 0 implies that positive Pki is positive definite and that reaching condition (24) is satisfied for all initial power demand for m = 2, thereby ensuring convergence of PES dynamics after the second module is activated following the load transient. (b) and (c) Experimental validations of reachability and stabilization of the currents.

Fig. 5: Post-transient stability of the distributed PES after a load transient from 0.6 kW to 1.4 kW. Initially one module feeds the load from the stack and subsequently after the transient, two modules are activated that feeds the additional power from the battery. (a) Minimum eigenvalue of Pki > 0 implies that positive Pki is positive definite and that reaching condition (24) is satisfied for all initial power demand for m = 3, thereby ensuring convergence of PES dynamics after the second module is activated following the load transient. (b) and (c) Experimental validations of reachability and stabilization of the currents.

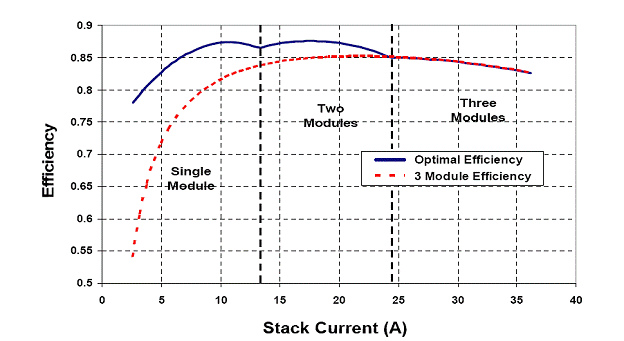
Fig. 6: Experimental comparison of the PES efficiency with varying stack current level. (top trace) Efficiency when m is varied between 1 through 3 following the optimal criterion outlined in Section II.A. When m = 2 or m = 3, the current is shared equally among the modules. (bottom trace) Efficiency when m is always 3 (i.e. no optimal power management implemented) and all the modules share current equally. Clearly, the former demonstrates flatter efficiency profile of the PES leading to better fuel-cell-stack utilization in steady-state.
management strategy leads to flatter and higher efficiency of the PES for most part along with convergence of the post-load-transient PES dynamics for varying load conditions. Overall, the distributed-PES-based power-management-control scheme leads to enhanced source utilization due to better PES efficiency profile and reduces (as compared to typical conventional approach) the requirements of footprint space, weight, and cost for battery-buffering by significantly reducing the requirement for a dedicated full-power-rating converter for the battery.
APPENDIX
A. Specifications and Test Conditions Of The Experiment
Stack Specifications

PES Specifications

References:
REFERENCES FOR CHAPTER 1
[1] Erdle, E., Gross, J., Muller, H.G., Müller, W.J.C., Reusch, H.J., and Sonnenschein, R., 1991, Proceedings of Second International Symposium on SOFCs, Edited by Singhal et al., pp. 265.
[2] Ferguson, J.R., 1991, “Analysis of temperature and current distributions in planar SOFC designs,” Proceedings of Second International Symposium on SOFCs, Edited by Singhal et al., pp. 305.
[3] Ferguson, J.R., Fiard, J.M., and Herbin, R., 1996, “A mathematical model of solid oxide fuel cells”, Journal of Power Sources, vol. 58, pp. 109-122.
[4] Hartvigsen, J., Elangovan, S., and Khandkar, A., 1993, Science and Technology of Zirconia V, Edited by Badwal, S., Bannister, M., and Hannink, R., Technomic Publishing Company, Inc., Lancaster, Pennsylvania.
[5] Kays, W.M., and London, A.L., 1998, Compact Heat Exchangers, Krieger Publishing Company, Malabar, Florida.
[6] Khaleel, M., Koeppel, B., and Moorehead, S., 2004, “Modeling and control of a solid oxide fuel cell auxiliary power unit”, 2004 DOE Hydrogen, Fuel Cells & Infrastructure Technologies. http://www.eere.energy.gov/hydrogenandfuelcells/pdfs/review04/fc_48_khaleel_04.pdf.
[7] Lee, F.C., 1990, “Modeling, analysis, and design of PWM converter”, Virginia Power Electronic Center Publications Series, Blacksburg, Virginia.
[8] Mazumder, S.K., Nayfeh, A.H., and Boroyevich, D., 2001, “Theoretical and experimental investigation of the fast- and slow-scale instabilities of a dc-dc converter”, IEEE Transactions on Power Electronics, vol. 16, no. 2, pp. 201–216.
[9] Mazumder, S.K., Acharya, K., Haynes, C.L., Williams, R., von Spakovsky, M.R., Nelson, D.J., Rancruel, D.F., Hartvigsen, J., and Gemmen, R.S., 2004, "Solid-oxide-fuel-cell performance and durability: resolution of the effects of power-conditioning systems and application loads", Special Issue on Distributed Generation, IEEE Transactions of Power Electronics, vol. 19, pp. 1263 - 1278.
[10] Middlebrook, R.D., and Cuk, S., 1977, “A general unified approach of modeling switching-converter power stages”, IEEE Power Electronics Specialists Conference, pp. 521-550.
[11] Mohan, N., Undeland, T.M., and Robbins, W.P., 1995, Power electronics: converters, applications & design, John Wiley & Sons, Second Edition, ISBN: 0471584088.
[12] Rancruel, D., 2005, Dynamic Synthesis/Design and Operation/Control Optimization Approach Applied to a Solid Oxide Fuel Cell based Auxiliary Power Unit under Transient Conditions, Ph.D. Dissertation, Virginia Polytechnic Institute and State University, Blacksburg, VA.
[13] Redl, R., Sokal, N.O., and Balogh, L., 1990, “A novel soft-switching full-bridge dc-dc converter; analysis, design considerations, and experimental results at 1.5kW, 100kHz”, IEEE Applied Power Electronics Conference, pp. 162-172.
[14] Shah, R.S., 1981, “Compact heat exchanger design procedure”, in Kakaç, S., Bergles, A. E., and Mayinger, F. (Editors), Heat Exchangers, Thermal-Hydraulic Fundamentals and Design, Hemisphere Publishing Corporation, Washington, pp. 495-536.
[15] Yentekakis, I.V., Neophytides, S., Seimanides, S., and Vayenas, C.G., 1993, “Mathematical modeling of cross-flow, counter-flow and cocurrent-flow solid oxide fuel cells: theory and some preliminary experiments”, Proceedings of 2nd International Symposium on Solid Oxide Fuel Cells, Athens, Greece, Official. Publication of the EEC, Luxembourg, pp. 281-288.
REFERENCES FOR CHAPTER 2
[1] “Assessment of fuel cells as auxiliary power systems for transportation vehicles”, Hydrogen and Fuel cells Merit Review Meeting, Berkeley, CA, 2003, http://www.tiax.biz/industries/pdfs/fuelcells/fc-apus_0114-03.pdf.
[2] Kim, J. W., Virkar, A. V., Mehta, K., Fung, K. Z., and Singhal, S.C., 1999, “Low Temperature, High Performance Anode Supported Solid Oxide Fuel Cells”, Journal of Electrochemical Society, 146(1), pp. 69-78.
[3] Khaleel, M.A., Recknagle, K.P., Lin, Z., Deibler, J.E., Chick, L.A., and Stevenson, J.W., 2001,“Thermo-Mechanical and Electrochemistry Modeling of Planar SOFC Stacks”, Electrochemical Society Proceedings, 2001-16, pp. 1032-1041.
[4] Hsiao, Y. C. and Selman, J. R., 1997, “The Degradation of SOFC Electrodes,” Proceedings of Solid State Ionics, 98, pp. 33-38.
[5] Huang, X. and Reifsnider, K., 2001, “Modeling Long-Term Performance of Solid Oxide Fuel Cells: A Phenomenological Approach,” 15th Annual Conference of Fossil Energy Materials, Knoxville, TN.
[6] Achenbach, E., “Response of a Solid Oxide Fuel Cell to Load Change,” Journal of Power Sources, 57, pp. 105 –109, 1995.
[7] Hartvigsen, J., Elangovan, S., and Khandkar, A., 1993, Science and Technology of Zirconia V, Edited by Badwal, S., Bannister, M., and Hannink, R., Technomic Publishing Company, Inc., Lancaster, Pennsylvania.
[8] Gemmen, R. S., 2003, “Analysis for the Effect of Inverter Ripple Current on Fuel Cell Operating Condition,” Journal of Fluids Engineering, 125(3), pp. 576 - 585.
[9] Acharya, K., Mazumder, S. K., Burra, R. K., Williams, R., and Haynes, C. L., 2003, “System-Interaction Analyses of Solid Oxide Fuel Cell (SOFC) Power-Conditioning System,” Proceedings of the IEEE IAS Conference, pp. 2026 – 2032.
[10] Acharya, K., Mazumder, S. K., Burra, R. K., 2004, “Impact of Power-Electronics Systems on the Performance and Durability of Tubular Solid-Oxide Fuel Cell”, Proceedings of the IEEE Applied Power Electronics Conference, 3, pp. 1515 - 1520.
[11] Mazumder, S.K., Acharya, K., Haynes, C.L., Williams, R., von Spakovsky, M. R., Nelson, D. J., Rancruel, D. F., Hartvigsen, J., and Gemmen, R. S., 2004, “Solid-Oxide-Fuel-Cell Performance and Durability: Resolution of the Effects of Power-Conditioning Systems and Application Load,” Special Issue on Distributed Generation, IEEE Transactions of Power Electronics, 19, pp. 1263 - 1278.
[12] Ferguson, J.R., Fiard, J.M., and Herbin, R., 1996, “A Mathematical Model of Solid Oxide Fuel Cells,” Journal of Power Sources, 58, pp. 109 – 122.
[13] Yentekakis, I. V., Neophytides, S., Seimanides, S., and Vayenas, C. G., 1993, “Mathematical Modeling of Cross-Flow, Counter-Flow and Cocurrent-Flow Solid Oxide Fuel Cells: Theory and Some Preliminary Experiments”, Proceedings of 2nd International Symposium on Solid Oxide Fuel Cells, Athens, Greece, Official. Publication of the EEC, Luxembourg, pp. 281- 288.
[14] Erdle, E., Gross, J., Muller, H.G., Müller, W.J.C., Reusch, H.J., and Sonnenschein, R., 1991, Proceedings of Second International Symposium on SOFCs, Edited by Singhal et. al., pp. 265-267.
[15] Ferguson, J. R., 1991, Proceedings of Second International Symposium on SOFCs, Edited by Singhal et. al., pp. 305-309.
[16] Hendrikson, P. V., 1994, Second Nordic Symposium on High Temperature Fuel Cells, Edited by T. Nordby and F. W. Poulsen, The Nordic Energy Research Programme and University of Oslo, Norway.
[17] Constantinides, A., and Mostoufi, N., 1999, Numerical Methods for Chemical Engineers with Matlab Applications, Prentice Hall PTR, Upper Saddle River, NJ.
[18] Erickson, R. W. and Maksimovic, D., 2004, Fundamentals of Power Electronics, Second Edition, Kluwer Academic Publishers, Massachusetts.
[19] Lee, F. C., 1990, Modeling, Analysis, and Design of PWM Converter, Virginia Power Electronic Center Publications Series, Blacksburg, Virginia.
[20] Yakabe, H., Ogiwara, T., Hishinuma, M., and Yasuda, I., 2001, “3D Model Calculation for Planar SOFC,” Journal of Power Sources, 102, pp. 144 -154.
[21] Stolten, D., 2004, “Comparison of SOFC and High Temperature Electrolysis,” High Temperature Electrolysis IEA Meeting, San Antonio
REFERENCES FOR CHAPTER 3
[1] Achenbach, E.A., 1995, “Response of a solid oxide fuel cell to load change” Journal of Power Sources, vol. 57, pp. 105-109, 1995.
[2] Boyd, S. and Vandenberghe, L., 2004, Convex Optimization, Cambridge University Press, New York.
[3] Brogan, W.L., 1990, Modern Control Theory, Prentice Hall, Upper Saddle River, New Jersey.
[4] Droppo, G.W., Schienbein, L.A., Harris, B.E., and Hammerstorm, D.J., 2003, “DC to DC converter and power management system”, U.S. Patent 6 628 011.
[5] Early, J. and Werth, J., 1990, “Fuel cell/battery control system”, U.S. Patent 4 961 151.
[6] Gemmen, R., 2003, “Analysis for the effect of inverter ripple current on fuel cell operating condition,” Journal Fluids Engineering, vol. 125, no. 3, pp. 576–585.Gao, L., Jiang, Z., and Dougal, R.A., 2005, “Evaluation of active hybrid fuel cell/battery power sources”, IEEE Transactions on Aerospace and Electronic Systems, vol. 41, issue 1, pp. 346-355.
[8] Hochgraph, C. and Singh, P., 2004, “Method and system for fuel cell control”, U.S. Patent 6 794 844.
[9] Hsiao Y.C. and Selma, J. R., 1997, “The degradation of SOFC electrodes”, Proceedings of Solid State Ionics, vol. 98, pp. 33-38.
[10] International Rectifier, IR2103 datasheet, www.irf.com/productinfo/datasheets/data/ir2103.pdf.
[11] Jang, S.J., Lee, T.W, Lee, W.C, and Won, C.Y., 2004, “Bi-directional dc-dc converter for fuel cell generation system”, IEEE Power Electronics Specialists Conference, vol. 6, pp. 4722-4728.
[12] Jossen, A., Garche, J., Doering, H., Goetz, M., Knaupp, W., and Joerissen, L., 2005, “Hybrid systems with lead–acid battery and proton-exchange membrane fuel cell”, Journal of Power Sources, vol.144, pp. 395-401.
[13] Kambouris, C.A. and Bates, J.T., 2006, “Dc-dc converter for a fuel cell system”, U.S. Patent 7014 928 B2.
[14] M.S. Kennedy Corporation, MSK 4401 datasheet, http://www.mskennedy.com/client_images/ catalog19680/pages/files/4401re.pdf.
[15] Mazumder, S.K., Nayfeh, A.H., and Boroyevich, D., 2001, “Theoretical and experimental investigation of the fast- and slow-scale instabilities of a dc/dc converter”, IEEE Transactions on Power Electronics, vol. 16, no. 2, pp. 201-216.
[16] Mazumder, S.K. and Acharya, K., 2006, “Multiple Lyapunov function based reaching condition analyses of switching power converters,” IEEE Power Electronics Specialists Conference, pp. 2232-2239.
[17] Mazumder, S.K., Pradhan, S., Hartvigsen, J., Rancruel, D., and von Spakovsky, M.R., 2007, “Investigation of load-transient mitigation techniques for planar solid-oxide fuel cell (PSOFC) power-conditioning systems”, IEEE Transaction on Energy Conversion, vol. 22, no. 2, pp. 457-466.
[18] Nesterov, Y. and Nemirovskii, A., 1995, “An interior-point method for generalized linear-fractional problems,” Springer Journal on Mathematical Programming: Series B, vol. 69, no. 1, pp. 177-204.
[19] Pradhan, S., Mazumder, S.K., Hartvigsen, J., and Hollist, M., 2007, “Effects of electrical feedbacks on planar solid-oxide fuel cell”, ASME Journal of Fuel Cell Science and Technology, vol. 4, no. 2, pp. 154-166.
[20] Pradhan, S., 2007, Modeling, analysis and control of effects of the electrical feedbacks on PSOFC power conditioning system, Doctoral Dissertation, Department of Electrical and Computer Engineering, University of Illinois at Chicago, Chicago, Illinois.
Journal Articles on this Report : 2 Displayed | Download in RIS Format
| Other project views: | All 4 publications | 2 publications in selected types | All 2 journal articles |
|---|
| Type | Citation | ||
|---|---|---|---|
|
|
Balci K, Yapar G, Akkaya Y, Akyuz S, Koch A, Kleinpeter E. A conformational analysis and vibrational spectroscopic investigation on 1,2-bis(o-carboxyphenoxy) ethane molecule. Vibrational Spectroscopy 2012;58:27-43. |
R831581 (Final) |
Exit Exit |
|
|
Mazumder SK, Pradhan S. Efficient and robust power management of reduced cost distributed power electronics for fuel-cell power system. Journal of Fuel Cell Science and Technology 2009;7(1):011018. (11 pp.). |
R831581 (Final) |
Exit Exit |
Supplemental Keywords:
Sustainable Industry/Business, RFA, Scientific Discipline, TREATMENT/CONTROL, INTERNATIONAL COOPERATION, POLLUTION PREVENTION, Technology for Sustainable Environment, Sustainable Environment, Environmental Chemistry, cleaner production/pollution prevention, Environmental Engineering, Technology, Energy, alternative energy source, emissions control, power electronics subsystems, fuel cell energy systems, cleaner production, energy efficiency, clean technologies, innovative technology, system interaction analysesProgress and Final Reports:
Original AbstractThe perspectives, information and conclusions conveyed in research project abstracts, progress reports, final reports, journal abstracts and journal publications convey the viewpoints of the principal investigator and may not represent the views and policies of ORD and EPA. Conclusions drawn by the principal investigators have not been reviewed by the Agency.
Project Research Results
Site Navigation
Related Information
Contact Us to ask a question, provide feedback, or report a problem.
Last updated April 28, 2023
