Grantee Research Project Results

2010 Progress Report: Understanding and Managing Risks Posed by Brines Containing Dissolved Carbon Dioxide

EPA Grant Number: R834383
Title: Understanding and Managing Risks Posed by Brines Containing Dissolved Carbon Dioxide
Investigators: Falta, Ronald W. , Benson, Sally M. , Murdoch, Lawrence C.
Current Investigators: Falta, Ronald W. , Murdoch, Lawrence C. , Benson, Sally M.
Institution: Clemson University , Stanford University
EPA Project Officer: Aja, Hayley
Project Period: November 1, 2009 through October 31, 2012 (Extended to October 31, 2014)
Project Period Covered by this Report: January 1, 2010 through December 31,2010
Project Amount: $891,342
RFA: Integrated Design, Modeling, and Monitoring of Geologic Sequestration of Anthropogenic Carbon Dioxide to Safeguard Sources of Drinking Water (2009) RFA Text | Recipients Lists
Research Category: Targeted Research , Water

Objective:

Geologic disposal of supercritical carbon dioxide in saline aquifers and depleted oil and gas fields will cause large volumes of brine to become saturated with dissolved CO₂ at concentrations of 50 g/l or more. As CO₂ dissolves in brine, the brine density increases slightly. This property favors the long-term storage security of the CO₂ because the denser brine is less likely to move upwards towards shallower depths. In fact, one proposed strategy for reducing risk from CO₂ injection activities involves pre-dissolving the CO₂ into brine at the surface, and injecting this brine into the disposal formation. While dissolved phase CO₂ poses less of a threat to the security of shallower drinking water supplies, the risk is not zero. There are plausible mechanisms by which the CO₂-laden brine could be transported to a shallower depth, where the CO₂ would come out of solution (exsolve), forming a mobile CO₂ gas phase. This significant mechanism for drinking water contamination has received little attention, and there are basic science and reservoir engineering questions that need to be addressed in order to reduce risks to underground drinking water supplies.

Six main activities were identified in the research proposal:

1) Laboratory Experiments. Laboratory core experiments that flood cores with CO₂-saturated brines at reservoir pressure and temperature. These cores then are gradually depressurized, and imaged using a medical CT scanner to study the CO2 phase evolution and movement.

2) Pore-Scale and Core-Scale Modeling. Pore-scale multiphysics and multiphase continuum modeling of these experiments are used to develop a fundamental understanding of the exsolution and CO₂ bubble coalescence phenomena as the CO₂ starts to form a mobile phase.

3) CO₂ Phase Relative Permeability Functions for Multiphase Flow Models. Core-scale multiphase continuum modeling to upscale the experimental results with a focus on developing effective relative permeability functions for use in field-scale modeling.

4) Regional-Scale Variable Density Groundwater Modeling. Simulations of regional scale behavior using a variable density groundwater flow model. The simulations are designed to evaluate the effects of upward hydraulic gradients, upward pressure driven brine flow (for CO₂ brine injection projects) and most importantly, the effects of groundwater pumping from shallower aquifers.

5) Multiphase Flow Simulations of Field-Scale CO₂ Injection. Local field-scale (hundreds to thousands of meters) multiphase simulations of the likely failure modes using realistic hydrogeologic and geologic conditions that are representative of CO₂ storage locations.

6) Remediation Designs. These models will then be used to study remediation strategies and alternative storage methods for each CO₂ release scenario.

Progress Summary:

During our first year on this project, we have made very good progress on Activities 1, 3, and 5. We have begun work on Activities 2 and 4, but have not yet started on Activity 6. A detailed summary of progress by activity area is provided in this report.

1. Laboratory Experiments

The laboratory apparatus is up and running, and several exsolution experiments have been conducted on Berea sandstones. Two different approaches to these measurements have been used. Both demonstrate the emergence of gaseous CO2 (exsolved CO2) when the pressure decreases. The second method also allows measurement of the relative permeability to CO2 and water in the presence of exsolved CO2.

Approach One—Rapid Depressurization: Core samples were initially filled with CO2 saturated water at 50° C and 1800 psi. After this, fluids were extracted as fast as possible (~100 psi/min) until the pressure dropped to a specified value. The core holder was then sealed and the system was monitored for 6 to 24 hours to observe equilibration of exsolved CO2 under the influence of gravity and capillary forces. This experiment was conducted using both homogeneous and heterogeneous samples of Berea sandstone.

Evolution of significant amounts of exsolved CO2 was observed in these experiments. CO2 saturations in core samples were 3%~5% at 1400 psi, 10%~15% at 1000 psi, 20%~27% at 800 psi, and 40%~46% at 400 psi. Exsolved CO2 had uniform distributions in homogeneous core samples but showed more complexity in heterogeneous core samples due to permeability variations and flow preference, shown in Figure 1.1. No statistically significant correlation between porosity and CO2 saturation was observed either before or after equilibration. No obvious upward migration of CO2 occurred during the pressure drop, nor during the equilibration period.

Multiphase flow simulation results using TOUGH2-ECO2N, based on measured core sample porosity, using a capillary curve and CO2/water relative permeability curve from a traditional core flooding experiment are shown in Figure 1.2. A reasonable, though imperfect match between the simulated and measured saturation distribution was observed after the pressure was dropped to 400 psi.

Although these experiments clearly demonstrated the exsolution of CO2, they provided little information about the mobility of exsolved CO2.

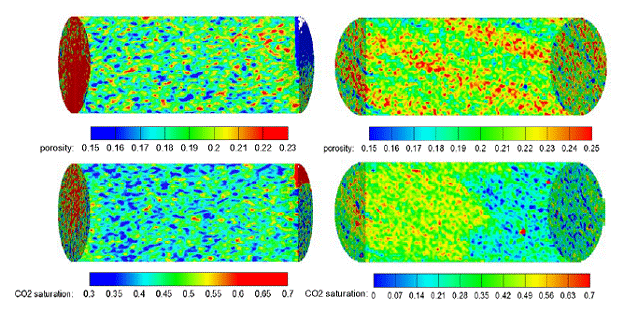Figure 1.1. CO2 distributions compared with porosity distributions of homogeneous rock (left) and heterogeneous rock (right) at 400 psi.

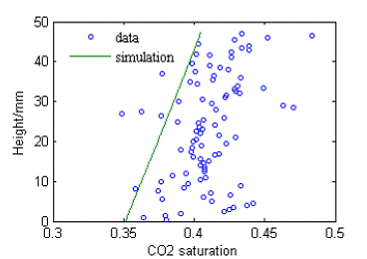Figure 1.2. CO2 distribution in the vertical direction of the middle rock slice compared with numerical simulation result 6 hours after initial pressure drop.

Approach Two—Slow Depressurization: These experiments were designed to provide more information about the mobility (relative permeability) of exsolved CO2 and water. Highly permeable Berea sandstone was used in these experiments. The core sample initially was filled with CO2 saturated water at 50° C and 1600 psi. The pressure was raised to 1800 psi. Following this, fluids were extracted from one end of the core holder at a sequence of constant withdrawal rates until pressure dropped to a specified value. With CT scanning and pressure drop measurements across the core, we were available to calculate relative permeabilities of CO2 and water based on mass balance. Equilibrations after pressure drops also were allowed to observe CO2 re-distribution in the core.

With much slower pressure drops compared to the first part, CO2 saturations in core samples were 3%~6% at 1200 psi, 6.5%~10% at 1000 psi, 13%~17% at 800 psi, and 41%~43% at 400 psi. The critical gas saturation, when the CO2 phase became mobile, was 11.7%~15.5% at core sample pressure 815 psi to 845 psi. This result has very significant implications for the security of dissolved CO2, because it shows that if the brine is depressurized, and the CO2 exsolves, that it does not become mobile until a high CO2 phase saturation is reached. This is much different than the behavior of separate phase CO2 movement when it is injected into a water filled rock. In that case, the CO2 phase can be mobile at much lower phase saturations because it preferentially seeks out the larger pore spaces in the porous media.

It is confirmed by repetitive scans that there is no correlation between CO2 saturation and porosity. Re-dissolution, rather than vertical re-distribution, appeared as equilibrium proceeded, shown in Figure 1.3.

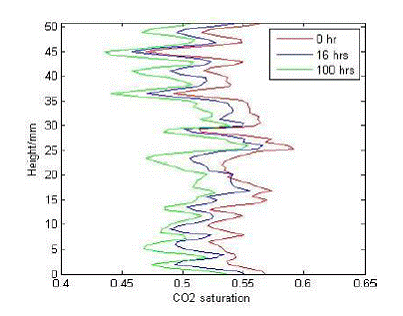Figure 1.3. Vertical CO2 distributions of the middle rock slice as equilibrium proceeded.

The measured relative permeability curves (Figure 1.4) show the relative permeability of water was reduced to less than 0.1 once exsolved CO2 appeared above a few percent saturation. More importantly, the relative permeability of the CO2 phase was very low (10^-5~10^-3), even when exsolved CO2 saturation increased to more than 40%. This result implies that even if CO2 exsolves from a depressurized brine, the resulting CO2 phase will have extremely low mobility in the formation. The significant reduction in both water and CO2 mobility observed in these experiments may form a kind of permeability barrier, which prevents CO2’s migration or even blocks possible leakage paths.

Figure 1.4 shows two repetitive relative permeability curve measurements for Berea sandstone. Poor repetition exists between two experiments, especially for CO2 curves. The measurement errors and the artifacts close to critical gas saturations were introduced primarily by measuring small pressure differential at low flow rates in the highly permeable core sample (966 mD). Further experiments will be conducted with core samples of lower permeability and at higher flow rates to reduce errors in pressure measurements.

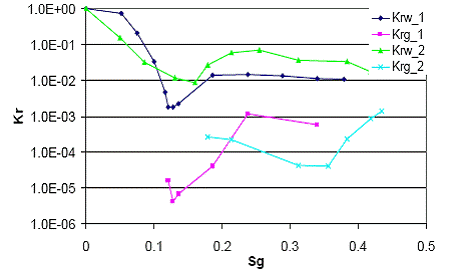Figure 1.4. Relative permeability curves of CO2 and water.

2. CO2 Phase Relative Permeability Functions for Multiphase Flow Models

Our work in this area so far has focused on the development and testing of new hysteretic relative permeability and capillary pressure functions for cases where supercritical or gas phase CO2 is moving through brine-filled porous media. As we have seen from the recent laboratory experiments, gas phase or supercritical CO2 that exsolves from a brine containing dissolved CO2 may behave much differently, and this will be a focus of our work during the coming year.

Characteristic curves that govern the interactions of immiscible phases in numerical flow simulators for environmental and petroleum applications often are used to model the flow of supercritical carbon dioxide during geologic carbon sequestration. These curves describe relative permeability and capillary pressure as functions of phase saturation in a multiphase simulation. Commonly used non-hysteretic characteristic curves follow only one path for wetting-phase drainage and imbibitions processes and are limited to using a single value for residual nonwetting phase saturation. Hysteretic characteristic curves take advantage of variable values of residual nonwetting phase saturation dependent on the history of the phase saturation in the respective grid-block. Hysteresis is critical to predicting the amount of trapped fluid phase when both wetting-phase drainage and imbibitions processes occur along a wide range of phase saturation values; such as when injected supercritical CO2 is subject to buoyant flow in a deep saline aquifer. We have developed a simple hysteretic model for characteristic curves that can be applied to environmental or carbon sequestration numerical modeling.

Multiphase flow numerical models, those used in the petroleum and environmental industries and those used for CO2 sequestration, use characteristic curves to describe the interactions of the separate phases. Characteristic curves are functions that describe capillary pressure–saturation and relative permeability–saturation relationships at the grid-block scale, and ultimately control the multiphase flow. Characteristic curves may differ between grid-blocks depending on the properties of the material each grid-block represents.

In a system consisting of two immiscible fluids in a porous medium, there exists an interface that distinguishes the two fluids as separate phases. This interface can shift through the pores as a response to pressure differences between the two phases, or capillary pressure (Pc). Increases in Pc can drive the nonwetting phase (the phase that does not preferentially adhere to solid surfaces) to advance into the pores, pushing the wetting-phase (the phase that preferentially adheres to solid surfaces) out while decreases in Pc reverse the process.

Figure 2.1 shows a typical non-hysteretic capillary pressure curve. As an increase in capillary pressure occurs, the model follows the branch upwards (wetting-phase drainage process) and wetting-phase saturation (Sw) can decrease until the irreducible wetting-phase saturation (Slr) is reached (signifying a complete wetting-phase drainage). A subsequent decrease in capillary pressure will cause the model to follow the branch back downwards (wetting-phase imbibition) as Sw increases. As long as the nonwetting phase saturation (Sn) reached at least the user-set value of Snr during wetting-phase drainage, the wetting-phase imbibition process can continue only until the Snr is reached. Otherwise, Sw can continue to increase to 1, leaving no residual nonwetting phase in the grid-block.

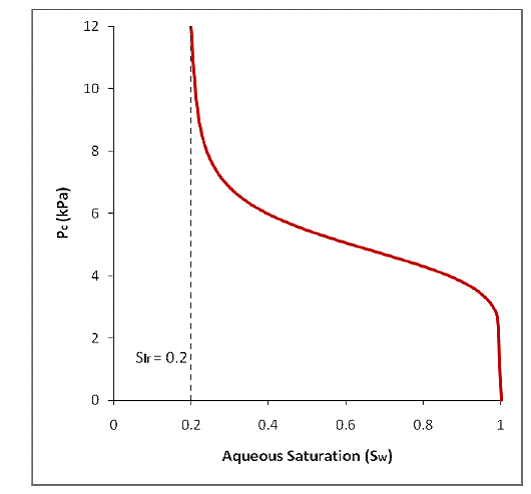
Figure 2.1. van Genuchten [1980] non-hysteretic capillary pressure curve.

A relative permeability curve is a function that controls the ease at which fluids may flow in a multiphase model. Relative permeability (kr) is a scaling factor (0–1) used to adapt the Darcy equation to multiphase flow (Equation 2.1). To clarify, a porous medium will have a specific conductivity value for a given fluid, e.g., water under single-phase conditions. The presence of a second fluid-phase, e.g., NAPL (non-aqueous phase liquid), however, in the pores of the medium will decrease the ease at which the water flows through the medium. Therefore, it is necessary to scale the fluid conductivity of the medium for each fluid phase to represent the competition of multiple phases for pore space fluid pathways.

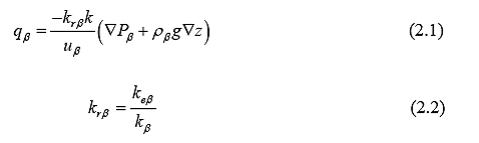
Equation 2.1 shows the Darcy equation for multiphase flow where qβ is the Darcy flux for phase β, , krβ is the relative permeability for phase β, μβ is the viscosity of phase β, and Pβ represents the pressure gradient within phase β. Equation 2.2 shows the relative permeability of phase β being equal to the ratio of the effective permeability of phase β (keβ) to the single-phase permeability of phase β.

Figure 2.2 shows a typical set of non-hysteretic relative permeability curves. As wetting-phase drainage occurs, the relative permeability of the wetting-phase (krw) decreases while the relative permeability for the nonwetting phase (krn) increases. The nonwetting phase relative permeability curve in this figure has a residual saturation (Snr) equal to zero, while the wetting phase curve has a residual saturation (Slr) of 0.2. With this nonwetting phase relative permeability curve, there is no trapping of the nonwetting phase, regardless of the flow history. Similar nonwetting phase relative permeability curves have been devised where a single fixed value of the nonwetting residual saturation is used. However, these tend to underpredict the nonwetting phase relative permeability when the phase first invades a water filled system, and they can over predict the mobility if the nonwetting phase is being displaced by water.

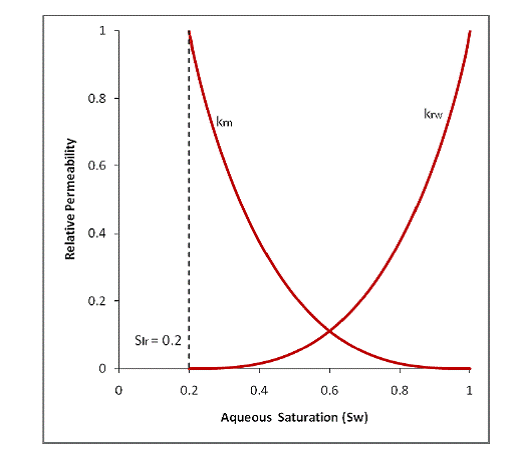Figure 2.2. Mualem [1976] non-hysteretic 2-phase relative permeability curve.

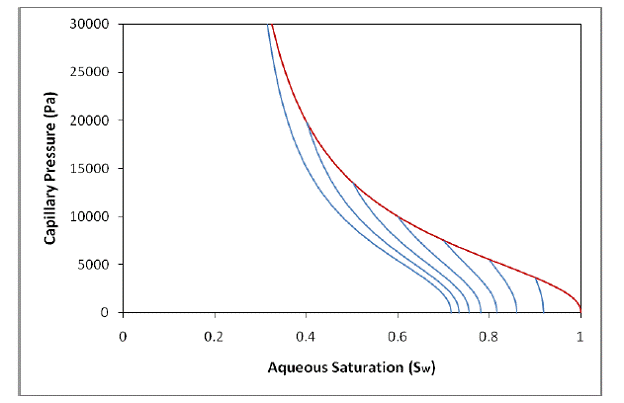
The characteristic curves in Figure 2.3 are hysteretic, meaning they describe the capillary pressure and relative permeability based not only on the current saturation but also on the history of saturation at the respective grid-block. These curves attempt to recreate the physical phenomenon known as hysteresis, where the amount of trapped fluid in the pores of a medium is dependent on the maximum amount of that fluid that initially entered the pores of the medium. Note the multiple wetting-phase imbibition branches for different

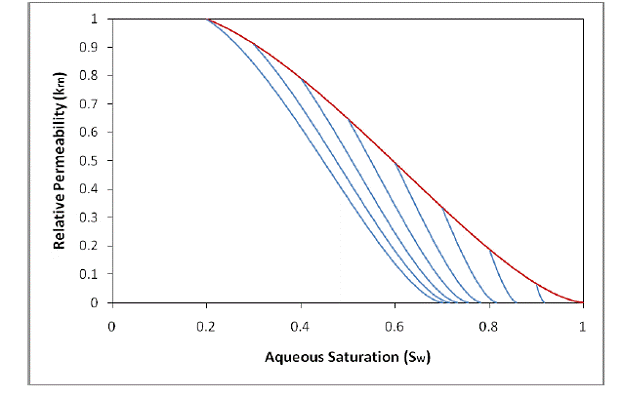Figure 2.3. Hysteretic characteristic curves from Kaluarachchi (1992). Notice from the multiple imbibition branches the value of Snr depends on the saturation at the turning point.

turning-point saturations (the saturation value at the point where the process changes from wetting-phase drainage to wetting-phase imbibition). The most important aspect of hysteretic characteristic curves is the calculation of Snr—represented as the value of Sn at which a wetting-phase imbibition branch has led to a Pc or krn value of 0—which varies depending on the maximum value of Sn reached during the wetting-phase drainage process. Greater values of Sn reached during wetting-phase drainage correspond to greater values of Snr.

The amount of fluid trapped at the pore scale affects the overall mobility of the fluid in the subsurface. When there exists both drainage and imbibition processes, e.g., during buoyancy-driven flow of supercritical CO2 through geologic media, the use of hysteretic values for residual saturation is critical to the behavior of the model. Hysteresis has been observed experimentally in problems involving NAPLs (e.g., Lenhard and Parker, 1987; Lenhard, 1992; Kueper, et al., 1993; Steffy, et al., 1997; Johnston and Adamski, 2005) and hysteretic characteristic curves have been developed and used for modeling in the petroleum and environmental industries.

A disadvantage of the hysteretic functions shown in Figure 2.3 is that the derivatives of the relative permeability and the capillary pressure are discontinuous at the turning points. In multiphase flow codes such as TOUGH2-ECO2N, this leads to numerical difficulties, and the curves must be artificially smoothed as the turning points are approached. As an alternative, we have developed a simple technique for incorporating the key hysteretic effects in relative permeability and capillary pressure curves. The resulting curves are always smooth, and continuously differentiable, leading to good numerical performance in TOUGH2-ECO2N.

Numerical Methods

The new method was used with a nonwetting phase relative permeability function (Equation 2.3) recently proposed by Charbeneau (2007). Effects of hysteresis are included through the calculation of Snr as a linear function (Equation 2.5) of the maximum nonwetting phase saturation (Snmax) in each grid-block. Experiment data for a NAPL-water system from Johnston and Adamski (2005) show residual nonwetting phase saturation to have a linear relationship with maximum nonwetting phase saturations Snmax. The slope of the linear function (ƒr) is dependent on the properties of the porous medium, increasing with finer-grained texture (Johnston and Adamski, 2005). Surface tension between differing fluids also may have an effect on the value of ƒr, although the need for further investigation exists.

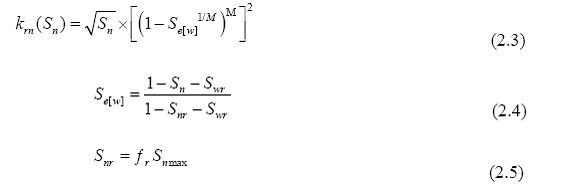In contrast to other hysteretic formulations (Kaluarachchi, 1992; Doughty, 2007; Fagerlund, et al., 2008) our model (Figure 2.4) calculates a non-zero Snr for the main wetting-phase drainage process. The value of Snr is updated continuously using the maximum Snmax value of the respective grid-block, regardless of the process. This ensures a continuous function at turning-point saturations. Although this alters the shape of the main drainage curve, the relative permeability curve parameters can be adjusted to move this curve as desired. As the nonwetting phase is displaced from its maximum value (wetting phase imbibitions), the nonwetting phase relative permeability smoothly approaches the residual saturation. In the case of CO2 dissolution, if the value of Sn drops below the value of Snr, Snmax is reset according to Equation 2.6.

The hysteretic trapping model was applied to a capillary pressure function based on van Genuchten’s equation (Equation 2.7). The linear trapping model is the same approach used for the calculation of Snr in the relative permeability model.

Figure 2.4 shows examples of the new hysteretic characteristic curves. Notice the continuous slope where the imbibition branches meet the main drainage branch—an effect of continuously updating the value of Snr during the wetting-phase drainage process. The curves in Figure 2.3 (Kaluarachchi’s hysteretic curves) were calculated using an Snr value of 0 for the main drainage and a non-zero value for imbibition—the effect of this abrupt calculation change can be seen by the discontinuous slope where the imbibition branches meet the main drainage branch.

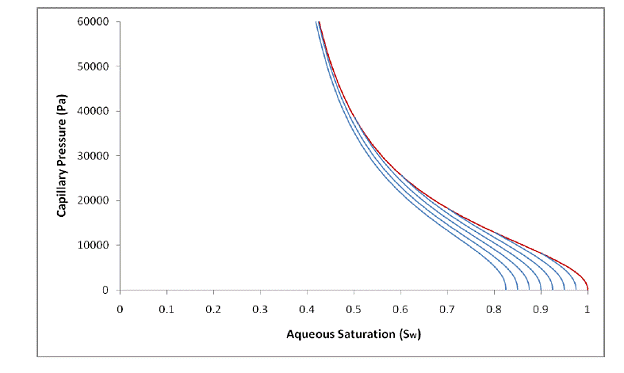
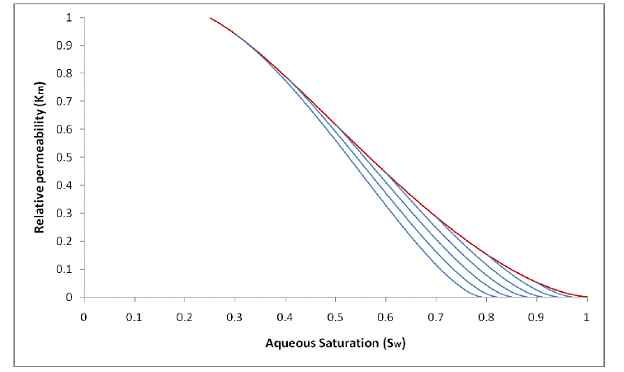
Figure 2.4. Examples of the new, smooth hysteretic characteristic curves.

Model Assessment

The first test made with the new hysteretic model was to simulate a NAPL/water experiment published by Johnston and Adamski (2005). The objective of their experiment was to explore the relationship between turning point saturation and residual NAPL saturation using a decane retention cell. Because this experiment involves nonwetting phase trapping in a two-phase system, it is physically similar to a CO2/water system, in which the CO2 is the nonwetting phase.

Figure 2.5 shows the set-up of their experiment. The retention cell held a core sample with a water reservoir connected to one end and a decane reservoir connected to the other end. A hydrophilic ceramic plate separated the core from the water reservoir while a hydrophobic ceramic plate separated the core from the decane reservoir. The plates were placed to ensure that decane would not leak into the water reservoir and that water did not leak into the decane reservoir. The pressure of the decane reservoir was held constant, while the pressure of the water reservoir was varied to apply and release suction to the core. The retention cell was subjected to cycles of subsequently increasing water suction to allow decane to flow into the core under increasing capillary pressures. The suction was released in between cycles to allow water to flow back into the core, pushing the decane out of the larger pores, leaving behind trapped nonwetting residual saturations.

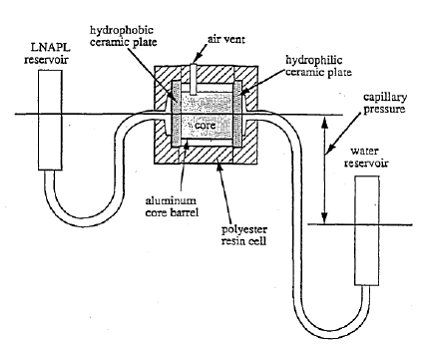
Figure 2.5. Diagram of a retention cell experiment. (Steffy, 1997)

The maximum saturation of decane measured in the core before suction was released was recorded as the turning point saturation, while the minimum saturation of decane measured in the core before suction was re-applied was recorded as the residual NAPL saturation. Over the span of about 90 days, 6 turning point saturation-residual NAPL saturation measurements were taken for the Texas City 3.66 – 4.27 m core sample (Figure 2.6). The measurements of residual NAPL saturations showed an approximate linear relationship with the measurements of the turning-point saturations (Figure 2.7). An estimate of 0.394 was given as the slope of the linear function (ƒr).

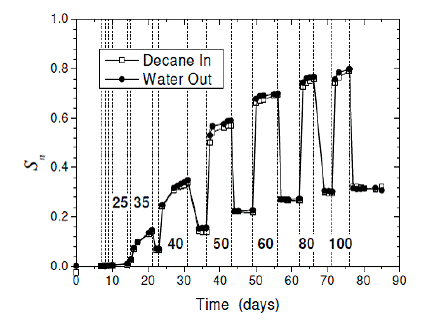
Figure 2.6. Residual saturation-turning point data for the Texas City 3.66-4.27 m core sample. Estimates of Sn were made from the measured amount of decane that flowed into the cell and the amount of water that flowed out of the cell. (Johnston and Adamski, 2005)

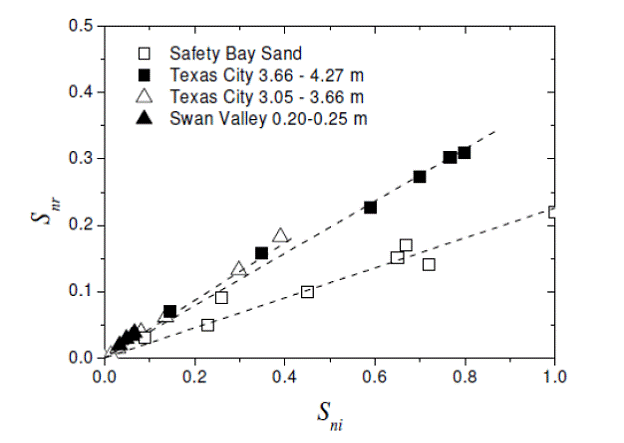
Figure 2.7. Residual nonwetting phase saturation (Snr) plotted against turning-point nonwetting phase saturation (Sni) from experimental data. (Johnston and Adamski, 2005)

Figure 2.8 shows the 1-dimensional model that was run with TMVOC version of TOUGH2 to simulate this experiment. The Texas City 3.66 – 4.27 m core sample was represented by ten grid-blocks in the center of the model, the ceramic plates were each represented by 2 grid-blocks on both ends of the core cells, and the reservoirs were each represented by 1 grid-block on both ends of the model. The cross-sectional area of the model was kept consistent with that of the core sample from Johnston and Adamski (2005). Because the hydraulic properties of the ceramic plates and the intrinsic permeability of the core sample were unknown, estimated values were used for these parameters in the simulation. The measured main drainage capillary pressure curve for the core sample was fit with Equation 2.7 and used in the model.

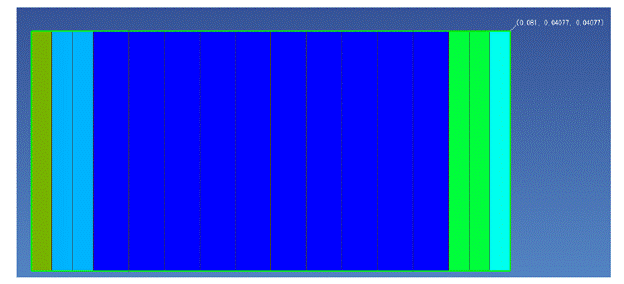
Figure 2.8. Model set-up for the experiment conducted by Johnston and Adamski (2005). The cells are colored according to material type.

The grid-blocks representing the hydrophilic plate were given a high nonwetting phase entry pressure in order to repel the decane, and the grid-blocks representing the hydrophobic plate were given a large negative capillary pressure to repel water. The grid-blocks representing the water and decane reservoirs were initially fully saturated in water and decane, respectively, and were held at the desired conditions—the decane reservoir grid-block kept at a constant pressure while the pressure of the water reservoir was controlled to match the experimental conditons. The actual times and values of pressure change were obtained through personal communication with Colin Johnston and were used in the pressure control for the water reservoir grid-block.

The value of ƒr from Johnston and Adamski (2005) was used to calculate Snr in the hysteretic relative permeability function. The fitted van Genuchten parameters from Johnston and Adamski (2005) were used for the capillary pressure function (which was not hysteretic in this simulation). Results from the simulation plotted with the experimental data are shown in Figure 2.9.

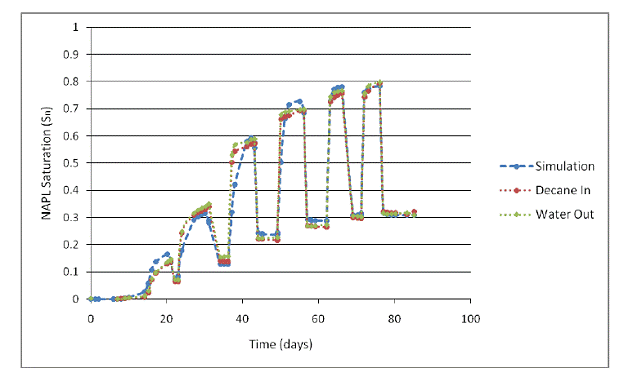
Figure 2.9. Experimental data from Johnston and Adamski [2005] plotted with the results from the TMVOC simulation using the new hysteretic nonwetting phase trapping model.

The second numerical test made with the new hysteretic model was to attempt to recreate a 2-dimensional hysteretic simulation of CO2 injection published by Doughty (2007). Doughty’s objective was to compare the behavior of a simulation of CO2 injection and leakage from the storage formation to the surface using her hysteretic characteristic curves and using typical non-hysteretic characteristic curves.

Doughty’s model was a 2-dimensional injection into a formation 100 m thick with leakage through an overlying formation 1000 m thick. Her model extended radially to 40,000 m, and was divided into 61 layers each with 41 grid-blocks. The layers were 20 m thick except for a few thinner layers near the surface. The grid-blocks were 20 m wide extending to 600 m, and then increased steadily to produce an infinite acting model. Both her injection formation and overlying formation were homogeneous, with a vertical permeability of 100 md and horizontal permeability of 200 md. The model was initially fully brine-saturated with a salinity of 100,000 ppm. The model followed a geothermal gradient of 30°C/km with the surface and bottom of the model held constant at 15°C and 48°C, respectively. Her simulation began by injecting 900,000 tons of CO2 for a period of 30 days, and simulation time continued to 1,000 years.

To ensure an accurate comparison of the behavior of our hysteretic formulations, Doughty provided the TOUGH2 input files for her simulation. It was noticed that her published simulations were carried out using ECO2, an older version of the TOUGH2 module ECO2N. The major difference between these modules is that ECO2N includes the density effect that CO2 has in the aqueous phase once dissolved. This turns out to have a dramatic effect on the results at late simulation times. Doughty also provided an updated simulation using ECO2N and shared her new (unpublished) results. Our comparison study will continue using these new simulation results.

We adjusted the parameter values in our relative permeability and capillary pressure curves so that the primary drainage curves are similar to those used in Doughty’s model. We also used a slightly different trapping model (the Land model) to be consistent with Doughty’s approach. The simulation results compare favorably (Figure 2.10), and confirm that the new and simplified hysteretic CO2 trapping function is able to reproduce the essential features of more complicated hysteretic models.

Over the next year, we plan to extend our work on relative permeability and capillary pressure functions to include the unique behavior that we have observed in the recent laboratory exsolution experiment.

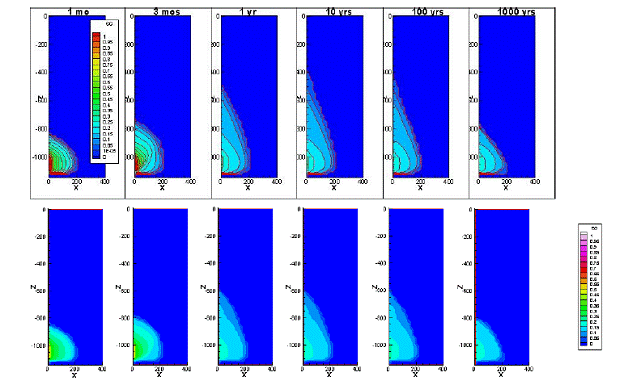
Figure 2.10. Results from Doughty (2007), top, and results from our new hysteretic model, bottom.

3. Pore-Scale and Core-Scale Modeling

Our efforts so far in this area have focused on continuum modeling of the laboratory experiments using TOUGH2-ECO2N (see Figure 2.2 above) for an example. As we develop new relative permeability functions, we will continue this type of core-scale modeling.

4. Regional-Scale Variable Density Groundwater Modeling

We have been performing studies to compare the numerical efficiency of the compositional multiphase flow simulator, TOUGH2, with the variable density groundwater flow and transport codes that are based on MODFLOW and MT3DMS. Although the TOUGH2 codes are designed for highly nonlinear multiphase flow problems, they can easily solve single phase variable density flow problems. Our initial comparisons show that it may be computationally feasible to run regional-scale groundwater modeling simulations using the TOUGH2 code. Use of these codes for the groundwater modeling part of this project would greatly simplify the overall modeling effort, because only a single modeling platform is needed to run both the multiphase flow and the groundwater flow simulations. Furthermore, we have parallel computing versions of the TOUGH2 code that can run on multiple processors. This allows us to make use of the Clemson Palmetto supercomputer (which has ~12,000 processors). Using this machine, we can run simulations on dozens to hundreds of processors.

5. Multiphase Flow Simulations of Field-Scale CO2 Injection

Our efforts on this task have been directed towards two main areas: 1) evaluation of dissolved CO2/brine transport from storage formations to drinking water formations through open abandoned wells, and 2) comparison of storage formation sweep efficiency and CO2 distribution during field-scale injection of supercritical versus dissolved CO2. These two areas are described below in separate sections.

A. Wellbore Leakage of Brines Containing Dissolved CO2

Introduction

In order to examine wellbore leakage, it is useful to explore the history of how wells have been completed and subsequently abandoned. Whenever a well is drilled, an open connected pathway is created between the surface and deep formations. Therefore, if wells are not properly sealed upon abandonment, there is potential for fluid migration up the wellbore, potentially contaminating overlying formations.

In the United States, oil and gas wells have been drilled for nearly 150 years. This has led to hundreds of thousands of wells that penetrate the subsurface. Because many of the suitable sites for carbon sequestration are depleted oil and gas formations or are in the vicinity of these formations, it is inevitable that abandoned wells will have to be dealt with when choosing sequestration sites.

Fortunately, many abandoned wells are not likely to pose a major leakage risk to sequestered CO2. Since 1952, well cements have had the appropriate additives to create a proper plug (Ide, et al., 2006). In addition, by the 1950s, most states had put in place sufficient well abandonment regulations. However, prior to this, well abandonment procedures were questionable. Before the 1950s, it is uncertain whether cement plugs were even effective. Early cements lacked the proper additives for the cement to harden at down-hole pressures and temperatures. In fact, such primitive techniques as pouring ice down the well to lower borehole temperature were used to try to achieve proper cementation. Furthermore, it is documented that many of the cement plugs from the Gulf Coast before the 1930s were contaminated with drilling mud (Smith, 1976).

In the early stages of oil and gas drilling, it is likely that many boreholes were abandoned without ever being effectively plugged. When early wells were plugged, they often were filled with whatever material was readily available. Well plugs discovered from the early 1900s have been found to contain materials such as logs, mud, and animal carcasses (Ide, et al., 2006).

Although many of these early wells are poorly sealed, many of them were drilled at relatively shallow depths. Therefore, they may not pose a serious risk to sequestration formations. However, poorly sealed wells do penetrate formations at a depth feasible for carbon sequestration (Gass, et al., 1977). Therefore, the possibility that gaseous CO2 may leak up them is a real concern. While leakage up a completely open wellbore may be unlikely, if CO2 does leak in this way, large volumes of CO2 could be released. In addition to leaking through these unsealed wells, it is possible that injected CO2 could degrade the integrity of properly sealed wellbores. Such leakage pathways include leakage through the cement, through corroded casing, and through the well annulus (Gasda, et al., 2004).

Over time, it is expected that injected CO2 will eventually dissolve into the storage formation brine with time-scales of hundreds to thousands of years (McPherson and Cole, 2000; Ennis-King and Paterson, 2003). In addition, some have proposed injecting CO2 as a dissolved phase (Burton and Bryant, 2007; Leonenko and Keith, 2008; Burton and Bryant, 2009). Fortunately, once CO2 is dissolved into storage formation brines, a buoyant gaseous CO2 phase no longer exists. In addition, upon dissolution, the brine becomes about 1% denser (Enick and Klara, 1990; Bachu and Adams, 2003); therefore, it will have a tendency to sink to the bottom of the formation.

While it seems less likely that dissolved CO2 will leak up abandoned wellbores, there is still a potential danger. If the storage formation is over pressured, or if an overlying aquifer is pumped, the pressure differential could force the dissolved CO2 upward through permeable pathways such as abandoned wells. As it rises, the CO2 has the potential to come out of solution as solubility decreases due to an increase in pressure.

Approach

In order to better understand the factors that control dissolved CO2 leakage such as well permeability, degree of overpressure, and well diameter, computer simulations were performed using the TOUGH2-ECO2N simulator (Pruess, 2007). In addition, a simple analytical model was developed to predict radial single-phase flow from a storage formation into a well, and then into a confined aquifer above. Although the analytical solution is only capable of calculating the volumetric flow rate of the aqueous phase, it is a useful predictive tool for estimating the order of magnitude of the effect of given parameters on the movement of brine containing dissolved CO2.

Analytical Model

The analytical model was developed by coupling steady state radial flow under Darcy’s law with linear Darcy or pipe flow in the wellbore. The well connects a storage formation to an overlying confined drinking water aquifer (DWA). In order to model a wide range of well conductances, from a completely open pipe to a permeability equal to the formations being modeled, two different wellbore flow models were used. For flow in a open or nearly open well, the Darcy-Weisbach equation for open pipe flow was used. For lower well permeabilities similar to the formation, Darcy’s law was used. The model assumes radial flow in both formations. Figure 5.1 shows a conceptual drawing of what the analytical model predicts as well as the variables used in the formula.

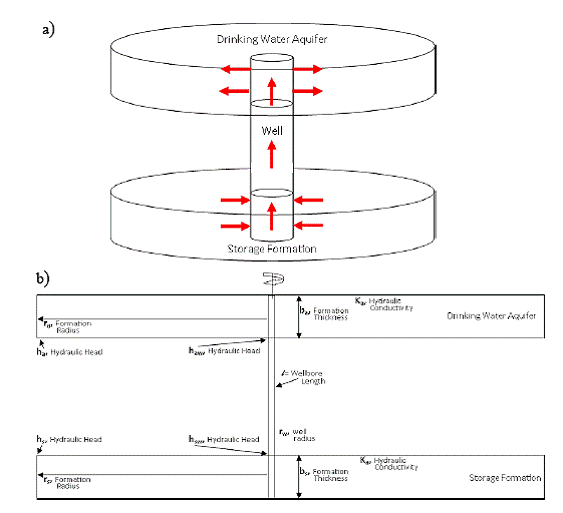
Figure 5.1. a) Arrows indicate the direction of flow in the analytical model. b) Drawing showing the variables used in the analytical model.

Solving for the radial volumetric flow rate (Q) into the well from the storage formation results in:

The radial flow out of the well into the DWA is similarly:

If the abandoned well is blocked enough to cause a significant flow resistance, Darcian flow up the well can be assumed:

These equations can be rearranged in terms of the head loss:

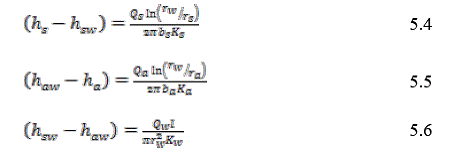
At steady state, Qs=Qa=Qw , and the sum of the three head drops (storage formation, well bore, DWA) is equal to the overall head difference between the storage formation and the DWA. Solving for the overall head drop gives:

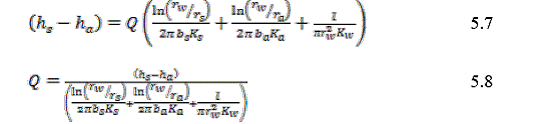
Equation 5.8 gives the water flow rate up the well as a function of the overall head difference between the two aquifers (assuming constant water density). The term multiplied by the head drop is the overall conductance of the system.

For instances where well permeabilities are high and the flow can no longer be assumed to be Darcian, the wellbore flow term (Equation 5.6) is replaced with the Darcy-Weisbach equation:

Where f is the Darcy-Weisbach friction factor (typically between 0.035-0.1) and g is acceleration due to gravity. Solving for the head drop as in Equation 5.7 results in the following quadratic equation:

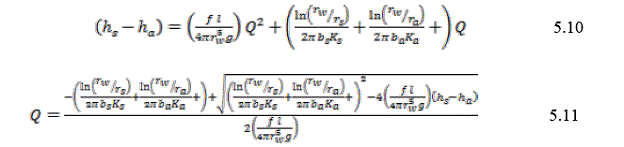
Both forms of the model are valid only for single phase aqueous flow of uniform density because hydraulic head is no longer applicable once the fluid density changes due to dissolution of CO2, the presence of brine, or variable temperature. Therefore, the model is not able to exactly predict the flow rate of CO2 laden brine into the DWA, especially if the CO2 comes out of solution. However, flow of CO2 dissolved in brine behaves as a single aqueous phase. Therefore, it is useful in estimating the sensitivity of different parameters on the overall leakage of CO2 up a leaking wellbore.

Numerical Model

The analytical model was helpful for designing a TOUGH2-ECO2N simulation to model dissolved CO2 movement up a leaking well to a drinking water aquifer. The sophistication of the ECO2N simulator allows for modeling the development of dissolved as well as a gaseous plumes in the DWA due to over pressurization of the storage formation and leakage through the well. A radially symmetric numerical grid design was selected for the TOUGH2-ECO2N simulations. Figure 5.2 shows the design of the numerical model.

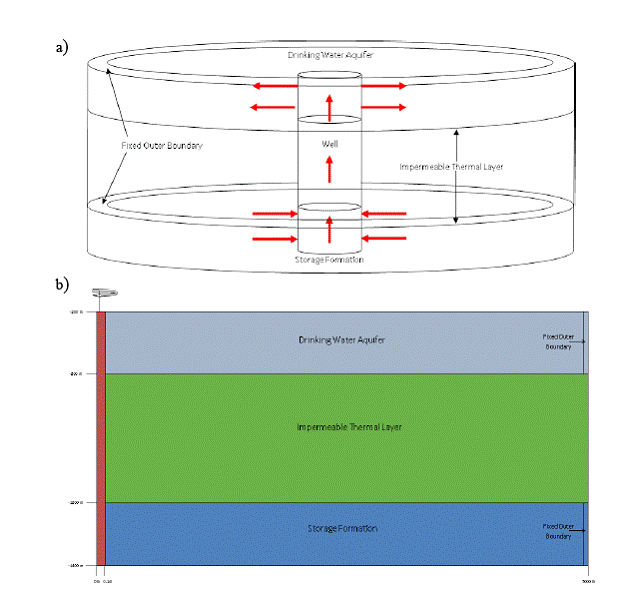
Figure 5.2. a) Drawing showing the design of the numerical model. b) 2-d representation of the materials used in the simulation.

The model’s outer radius was set to 5,000 meters so that any developing leakage plumes could be contained inside the model and so that end effects could be minimalized. The model was given an overall vertical length of 1,200 meters. Both the storage formation and the drinking water aquifer are 100 meters thick. Between the two formations is a 1000 meter thick impermeable layer. The top of the model is set at a depth of 200 meters below the ground surface.

Hydrostatic pressure was used to generate the pressure gradient such that the pressure in the top formation is ≈2.0x10⁶ Pa and the bottom formation is ≈1.4x10⁷ Pa. In addition, a geothermal gradient of 30°C/km with a surface temperature of 15°C was used. This gradient is typical of the western United States and has been used in other numerical models (Pruess, 2008).

The impermeable layer represents a case where only flow between the storage formation and the DWA are considered. The layer does not transmit fluids, but it does allow for thermal conduction and dissipation of heat from the warmer storage formation water as it rises through the wellbore.

The wellbore consists of the center radial elements, which are given a different permeability from the surrounding elements.

The model was discretized by using 87 grid-blocks in the radial dimension. The thickness of each successive ring increases starting with the well radius (4"; 0.1 m) as the innermost grid-block and extending to a thickness of ≈95 m in the outermost ring. Beyond this outermost ring, a fixed state condition (constant pressure, temperature, concentration, and saturation) was maintained. This allows for flow into the storage formation as well as flow out of the DWA. In the z dimension, a total of 70 grid-blocks were used. The storage formation uses ten 10-meter thick model layers, while the DWA is more refined using twenty 5 meter thick model layers. The impermeable layer was given forty 25-meter thick model layers. This discretization results in a total of 6090 grid-blocks for the entire model.

Table 5.1 shows the material properties for the storage formation, the DWA, and the impermeable layer. All three layers have a rock density of 2600 kg/m³, wet heat conductivity of 2.51 W/m·°C, and a specific heat of 920 J/kg·°C.

Table 5.1. Material properties of the ECO2N model

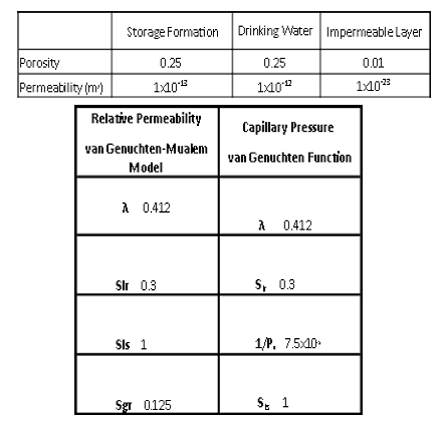The material properties do not represent any exact geologic location but instead represent typical properties for potential carbon sequestration sites. The relative permeability and capillary pressure parameters come from Doughty, 2007.

For the wellbore, it was desired to minimalize relative permeability and capillary pressure effects. Therefore, the relative permeability parameters for the well were changed so that Slr and Sgr were both 0.02. Capillary pressure was set to zero. In addition, the well porosity was set very high to 0.98. The well permeability varies between simulations.

Results

Analytical Model

In order to test the reliability of the analytical model, the numerical model was used to run simple flow tests with pure water. The volumetric flow rates observed in the numerical model then were compared to the analytical solution for accuracy.

The first comparison was the sensitivity of the flow rate to changes in well permeability. In the numerical model, the bottom formation was given an overpressure of 20 bars to induce flow up the well. Once steady state was obtained, the flow rates given by the model were compared to the calculated flow rate given by the analytical solution.

Table 5.2 shows good agreement between what is predicted by the analytical solution and the flow rate observed in the numerical model. The differences in the two models at lower well permeabilities are probably due to the fact the TOUGH2-ECO2N calculates the water density and viscosity as a function of pressure, while the analytical model assumes these parameters to be constant. The result from Equation 5.11, which uses the pipe flow equation also is shown. The numerical model uses Darcy’s law for all flows. For the case presented in Table 5.2, the overall conductance of the system becomes dominated by the formation conductances once the well permeability exceeds about 10^-6 m².

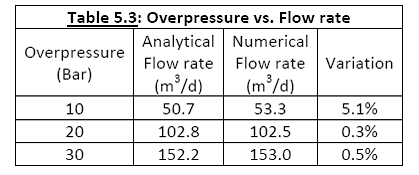
For another comparison, a numerical simulation was performed at three different storage formation overpressures. A well permeability of 1x10^-8 m² was used in both models. Table 5.3 shows good agreement between the numerical and analytical models at steady state.

Effects of Wellbore Permeability on Dissolved CO2 Leakage

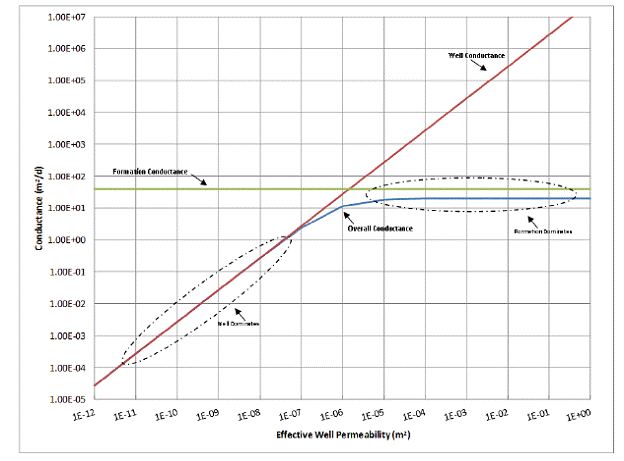
The conductance term in Equation 5.8 is useful for showing the effect of well permeability on the overall flow rate of water through the model. Conductance, which is the inverse of resistance, describes the ease with which the fluid can flow. Thus, the higher the conductance, the higher the flow for a given head difference. Figure 5.3 plots the individual conductances of formations with a permeability of 1x10^-12 m² and a wellbore of various permeabilities against the overall conductance of the entire model. This shows the effect of the wellbore permeability on the overall conductance. At well permeabilities below 1x10^-7 m² the overall conductance is dominated by the wellbore’s conductance. This indicates that the well is the most resistant portion of the model and therefore limits the flow rate. At higher well permeabilities, it can be seen that the overall flow rate is no longer dependent on the well permeability. Instead, the formations provide the most resistance to flow.

Figure 5.3. Model conductances as a function of the well permeability.

If the numerical model flow rate from Table 5.2 above is plotted against well permeability, it can be seen that the flow rate is controlled in the same way that the conductance term suggests (Figure 5.4), even though this model switches over to the pipe flow equation when the well permeability exceeds 10^-8 m². Over most of the range where the well permeability controls the overall flow rate, the analytical model suggests a 1:1 relationship between flow rate and well permeability. As can be seen in Table 5.2, when the permeability is increased by two orders of magnitude, the flow rate also increases by roughly the same amount. As the well becomes even more permeable, the formation begins to limit the flow rate. As a result, the increase in flow rate is minimal between higher well permeabilities because the formations are limiting the overall flow rate. This indicates that in a leakage scenario, the maximum possible flow rate of the leaking fluid is limited by the permeability of the formations it is flowing out of or into.

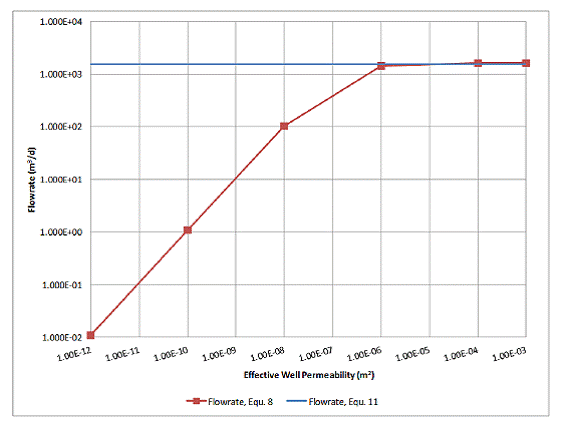
Figure 5.4. Flow rate as a function of well permeability.

The analytical model can predict only the behavior of constant density water moving up the wellbore, and it cannot account for CO2 exsolution in the wellbore or formation. Therefore, in order to see more realistically how dissolved CO2 will behave as it moves up the wellbore, the numerical model was used. In the ECO2N model, the storage formation was given a salinity of 2% by mass, which is representative of a low salinity brine. The CO2 concentration in the storage formation was 4.4% by mass. As can be seen in Figure 5.5, this solubility is slightly lower than the maximum solubility at the initial P/T conditions of the storage formation (≈1.4x10⁷ Pa; ≈55°C).

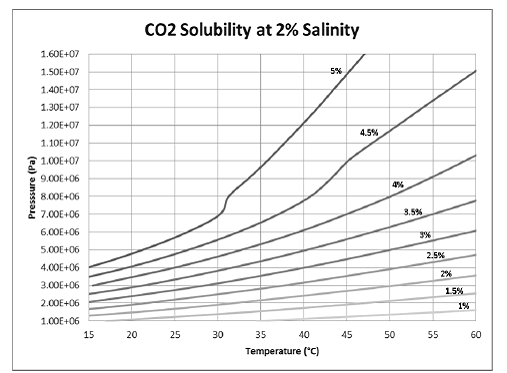Figure 5.5. Dependence of aqueous solubility of CO₂ on pressure and temperature.

Upward flow of dissolved brine was induced in all of the models by adding an additional 20 Bar (2x10⁶ Pa) of pressure on the storage formation. This overpressure is consistent with predicted overpressures due to CO2 injection, and it is approximately equivalent to a 200 m head increase. Zhou, et al. (2010) showed overpressures as high as 35 Bar after 50 years of CO2 injection in their models. A range of different well permeabilities was simulated starting with a permeability equal to the DWA of 1x10^-12 m², increasing to 1x10^-4 m².

After 50 years of overpressure, the CO2 moves up the wellbore and accumulates in the DWA. In addition to the dissolved phase leaking into the DWA, the CO2 also forms a separate gas phase near the top of the formation. As can be seen in Figure 5.5, CO2 solubility decreases as the dissolved CO2 rises vertically through the well and pressure drops. Therefore, the mass fraction of CO2 above the new solubility conditions will form a separate gas phase. In the model, the gas phase first appears in the lower portion of the wellbore and continues to increase in volume as pressure decreases up the wellbore. Figure 5.6 shows the dissolved CO2 plume as well as the separate gas phase that forms in the DWA due to leakage up the wellbore at various wellbore permeabilities.

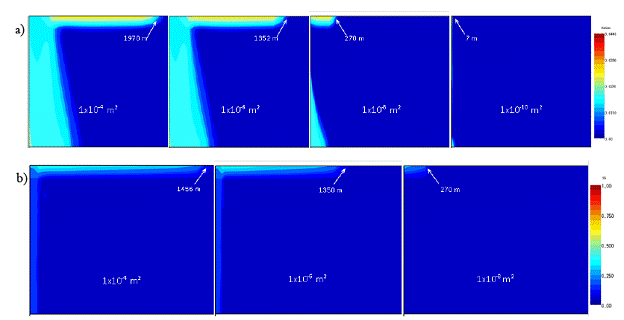
Figure 5.6. a) Dissolved CO2 plume in the drinking water aquifer at various well permeabilities at 50 years. b) Gas plume in the drinking water aquifer at 50 years. Vertical exaggeration is 1.5.

For all well permeabilities, the dissolved plume has two components to its shape. Horizontal accumulation at the top of the DWA is due to the gaseous CO2 dissolving into the resident water. The remainder of the plume represents the dissolved CO2 that has entered the formation through the wellbore. This plume is larger at the bottom of the formation because the dissolved brine is denser than the resident water of the DWA. The gaseous CO2 plume is concentrated largely along the top of the DWA due to its buoyancy and the fact that it comes out of the well at the top of the formation.

Figure 5.6 again illustrates that the amount of CO2 that escapes to the DWA is highly dependent on the well permeability up to a certain point. Table 5.4 and Figure 5.7 show the mass accumulation of CO2 in the DWA at 50 years. The mass accumulations plotted in figure 5.7 show the same dependence on permeability as Figure 5.4. At lower well permeabilities, the mass of CO2 that escapes to the DWA is dependent on the permeability of the well. As well permeability increases, the storage formation begins to limit the mass of CO2 that moves up the wellbore. In addition, as the analytical solution predicts, as the well permeability drops by an order of magnitude, so does the total mass accumulation of CO2.

Table 5.4. Well permeability (m²)

	1.00x10^-4	1.00x10^-6	1.00x10^-8	1.00x10^-10	1.00x10^-12
Gaseous CO₂ (kg)	1.14x10⁸	9.29x10⁷	2.30x10⁶	1.21x10³	0
Dissolved CO₂ (kg)	4.78x10⁸	3.76x10⁸	1.78x10⁷	2.09x10⁵	1.59x10³
Total CO₂ (kg)	5.92x10⁸	4.69x10⁸	2.01x10⁷	2.10x10⁵	1.59x10³

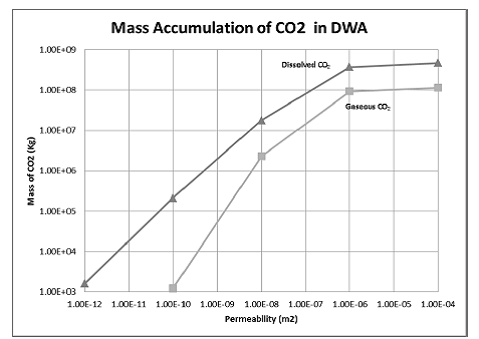
Figure 5.7. Mass accumulation of dissolved and gaseous CO₂ in the drinking water aquifer plotted as a function of well permeabilities at 50 years.

Effects of Wellbore Diameter on Dissolved CO2 Leakage

Many different types of wells have been drilled into potential sequestration sites and have the potential to be improperly sealed. In addition to oil and gas production wells, there are exploration wells, test borings, and many other well types (Gass, et al., 1977). Therefore, understanding CO2 leakage effects due to wellbore diameter is important. The ECO2N model again was used with the same properties of 2% salinity and 4.4% dissolved CO2. However, the model discretization was changed such that three different wellbore diameters could be modeled. The model was given a storage formation overpressure of 20 bar and a well permeability of 1x10^-8 m². Figure 5.8 shows the model and the dissolved phase plume in the DWA after 50 years of overpressure with different wellbore diameters. As the wellbore diameter increases, the amount of CO2 that leaks into the DWA increases as well. Table 5.5 compares the increases in total mass accumulation of CO2 after 50 years due to different well diameters. The table shows that the increase is closely related to the increase in the cross-sectional area of the well due to increasing diameter. Thus, doubling the wellbore cross-sectional area would in turn double the mass of CO2 leaked into the DWA.

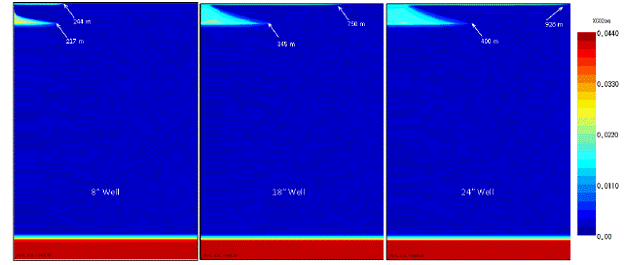
Figure 5.8. Mass accumulation of dissolved CO2 in the drinking aquifer at various well diameters.

Gaseous CO₂ (kg)

Dissolved CO₂ (kg)

Total CO₂ (kg)

Increase in Total Mass

Future Activities:

Research will be continued by comparing the analytical model to the results of the variable well diameter and overpressure numerical models.

It is plausible that dissolved CO2 could be forced up an abandoned well without the existence of storage formation overpressure. If an overlying aquifer that is connected to a formation containing dissolved CO2 is pumped, CO2 may be drawn up the abandoned well due to the drop in pressure of the overlying formation. The ECO2N model will be used to model this scenario and examine the effects.

In addition, the complexity of the numerical model will be increased by replacing the impermeable layer with a stratigraphic series of aquitards and aquicludes. This will allow for evaluation of leakage into formations other than just the topmost drinking water aquifer. Also, the effect of different capillary entry pressure and relative permeability properties in the DWA on CO2 leakage plumes will be explored.

To increase the accuracy of these sweep efficiency models, future simulations will include highly resolved grids and will be run using a parallel version of TOUGH2-ECO2N. The case of injection into a storage formation with heterogeneous, random, spatially correlated permeability fields will be run on a stratified regional scale. Hysteretic relative permeability and capillary pressure curves from Task 3 will be implemented. To reduce numerical error, the grid orientation effect of Voronoi grids versus rectangular grids will be compared in the case of supercritical CO2 injection.

Research will be continued by comparing the analytical model to the results of the variable well diameter and overpressure numerical models.

References:

Bachu, S. and J. J. Adams, 2003, Sequestration of CO2 in geological media in response to climate change: capacity of deep saline aquifers to sequester CO2 in solution, Energy Conversion and Management, vol. 44, no. 20, p. 3151-3175.

Burton, M. M. and S. Bryant, 2007, Eliminating Buoyant Migration of Sequestered CO2 through Surface Dissolution: Implementation Costs and Technical Challenges.

Burton, M. M. and S. L. Bryant, 2009, Surface dissolution: Minimizing groundwater impact and leakage risk simultaneously, Energy Procedia, vol. 1, no. 1, p. 3707-3714.

Charbeneau, R., 2007, LNAPL Distribution and Recovery Model (LDRM) Volume 1: Distribution and Recovery of Petroleum Hydrocarbon Liquids in Porous Media, American Petroleum Institute API Publication 4760.

Doughty, C., 2007, Modeling geologic storage of carbon dioxide: comparison of non-hysteretic and hysteretic characteristic curves, Energy Conversion and Management, 48(6):1768-1781.

Enick, R. M. and S. M. Klara, 1990, CO 2 solubility in water and brine under reservoir conditions, Chemical Engineering Communications, vol. 90, no. 1, p. 23-33.

Ennis-King, J. and L. Paterson, 2003, Rate of dissolution due to convective mixing in the underground storage of carbon dioxide, Greenhouse Gas Control Technologies.

Gasda, S. E., S. Bachu, and M. A. Celia, 2004, The potential for CO2 leakage from storage sites in geological media: analysis of well distribution in mature sedimentary basins, Environmental Geology, vol. 46, no. 6-7, p. 707–720.

Gass, T., J. Lehr, and H. Heiss Jr, 1977, Impact of abandoned wells on ground water.

Ide, S. T., S. J. Friedmann, and H. J. Herzog, 2006, CO2 leakage through existing wells: current technology and regulations, , p. 19-22.

Johnston, C., and M. Adamski, 2005, Relationship between initial and residual LNAPL saturation for different soil types, Proceedings of the 2005 Petroleum Hydrocarbons and Organic Chemicals in Groundwater®: Prevention, Assessment, and Remediation Conference. 17-19 August, Costa Mesa, 29-42.

Kaluarachchi, J.J., and Parker, J.C., 1992, Multiphase flow with a simplified model for oil entrapment, Transport in porous media, 7: 1, 1-14.

Kueper, B.H., D. Redman, R.C. Starr, S. Reitsma, and M. Mah, 1993, A field experiment to study the behavior of tetrachloroethylene below the water table: spatial distribution of residual and pooled DNAPL, Ground Water, 31: 5, 756-766.

Lenhard, R.J., and J.C. Parker, 1987, Measurement and prediction of saturation-pressure relationships in three-phase porous media systems, Journal of Contaminant Hydrology, 1, 407-424.

Lenhard, R.J., 1992, Measurement and modeling of three-phase saturation-pressure hysteresis, Journal of Contaminant Hydrology, 9, 243-269.

Leonenko, Y. and D. W. Keith, 2008, Reservoir engineering to accelerate the dissolution of CO2 stored in aquifers, Environ.Sci.Technol, vol. 42, no. 8, p. 2742-2747.

Mualem, Y., 1976, A new model for predicting the hydraulic conductivity of unsaturated porous media, Water Resources Research 12: 3, 513-522.

McPherson, B. and B. S. Cole, 2000, Multiphase CO2 flow, transport and sequestration in the Powder River basin, Wyoming, USA, Journal of Geochemical Exploration, vol. 69, p. 65-69.

Pruess, K., 2008, On CO 2 fluid flow and heat transfer behavior in the subsurface, following leakage from a geologic storage reservoir, Environmental Geology, vol. 54, no. 8, p. 1677-1686.

Pruess, K., 2007, ECO2N-A fluid property module for the TOUGH2 code for studies of CO2 storage in saline aquifers, Energy conversion and management, vol. 48, no. 6.

Steffy, D.A., D.A. Barry, and C.D. Johnston, 1997, Influence of antecedent moisture content on residual LNAL saturation, Soil and Sediment Contamination: An International Journal, 6: 2, 113-147.

Smith, D. K., 1976, Cementing, Society of Petroleum Engineers, Richardson, TX.

Zhou, Q., J. T. Birkholzer, E. Mehnert, Y. F. Lin, and K. Zhang, 2010, Modeling basin-and plume-scale processes of CO2 storage for full-scale deployment, Ground Water.

Journal Articles:

No journal articles submitted with this report: View all 16 publications for this project

Supplemental Keywords:

Relevant Websites:

Progress and Final Reports:

Original Abstract

The perspectives, information and conclusions conveyed in research project abstracts, progress reports, final reports, journal abstracts and journal publications convey the viewpoints of the principal investigator and may not represent the views and policies of ORD and EPA. Conclusions drawn by the principal investigators have not been reviewed by the Agency.